विषय-सूचि
चतुर्भुज की श्रेणी में इससे पहले हमनें समचतुर्भुज (rhombus) और समान्तर चतुर्भुज (parallelogram) के बारे में पढ़ा।
समलम्ब चतुर्भुज की परिभाषा (meaning of trapezium in hindi)
समलम्ब चतुर्भुज एक ऐसा चतुर्भुज होता है जिसकी दो भुजाएं समान्तर होती हैं। समलम्ब चतुर्भुज को हम अंग्रेजी में Trapezium कहते हैं।
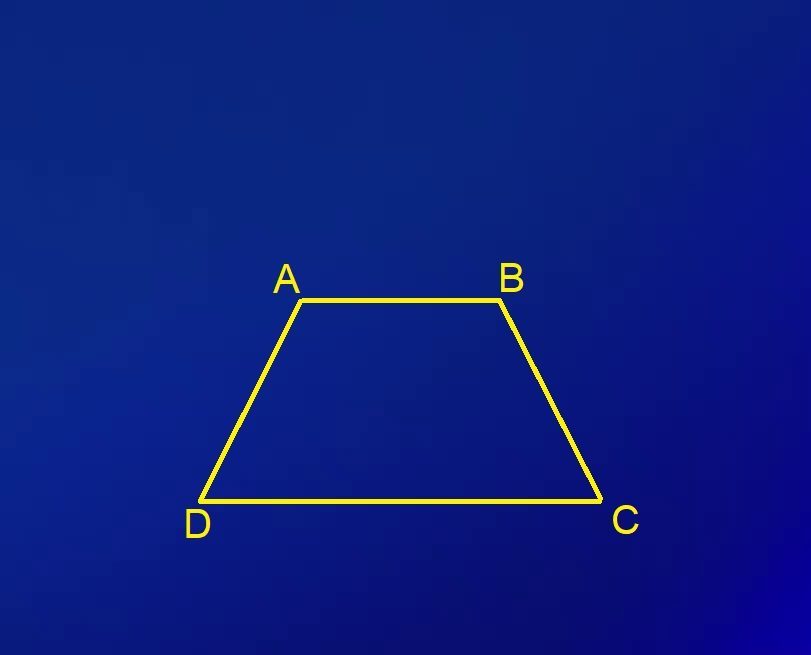
- जैसा कि आप ऊपर दी गयी आकृति में देख सकते हैं यहाँ हमारे पास ABCD एक आकृति है जिसकी दो भुजाएं समान्तर हैं एवं बची हुई दो भुजाएं समान्तर नहीं हैं। जैसा कि हमने ऊपर दी गयी परिभाषा में देखा की दो भुजाएं समान्तर होती हैं तो वह समलम्ब होता है अतः ऊपर दी गयी गयी आकृति भी समलम्ब होगी।
- हम देख सकते हैं की इस चतुभुज में कोई दो भुजाएं ही समान्तर होती हैं दूसरी दोनों भुजाएं एक दुसरे से समान्तर नहीं होती अतः यह एक समानांतर चतुर्भुज से इस तरह भिन्न होगा।
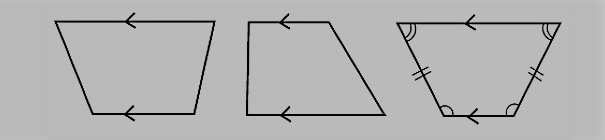
- ऊपर एक चित्र में कुछ आकृतियां दे रखी हैं। अगर हम इन्हे देखे तो पहली दो आकृतियों में सिर्फ एक युग की भुजाए समान्तर हैं इसलिए ये चतुर्भुज समलम्ब चतुर्भुज कहलायेंगे। लेकिन जो तीसरी आकृति है उसमे दो युगों की भुजाऐं एक दुसरे से समानांतर हैं इसलिए यह एक सामानांतर चतुर्भुज होगा।
ये भी पढ़ें:
समलम्ब चतुर्भुज के गुणधर्म (properties of trapezium in hindi)
- एक समलम्ब चतुर्भज की भुजाओं का सिर्फ एक युगल समानांतर होता है।

ऊपर दिए गए समलम्ब चतुर्भुज ABCD में जैसा कि आप देख सकते हैं की भुजाओं के दो में से सिर्फ एक ही युगल समान्तर है। दूसरा युगल माप में बराबर हो सकता है लेकिन समान्तर नहीं हो सकता है। समान्तर होने पर वह एक समानान्तर चतुर्भुज बन जाएगा।
- दो असमानान्तर भुजाओं के मध्य बिंदुओं को जोड़ने वाला एक रेखाखंड दो समान्तर भुजाओं के समानांतर होता है।
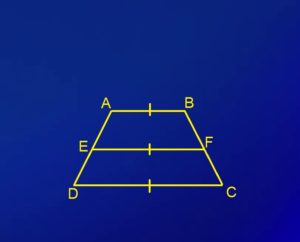
जैसा कि आप ऊपर देख सकते हैं यहाँ E एवं F क्रमश भुजा AD एवं BC के मध्य बिंदु है। इन मध्य बिन्दुओं को एक रेखा खंड EF जोड़ रहा है। हम देख सकते हैं यह रेखाखंड समान्तर भुजा के युगल के समान्तर है।
- दुसरे चतुर्भुजों की तरह समलम्ब चतुर्भुज में भी चारों कोणों का योग 360 अंश होता है।
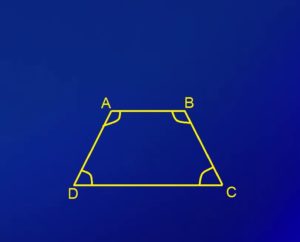
जैसा कि आप ऊपर देख सकते हैं यहाँ ABCD समलम्ब में कोण A + कोण B + कोण C + कोण D = 360 अंश होता है।
ये भी पढ़ें:
समलम्ब चतुर्भुज का क्षेत्रफल (area of trapezium in hindi)
हम एक समलम्ब का क्षेत्रफल ज्ञात करने के लिए सबसे पहले यह जानना होगा कि यह आकृति किन किन आकृतियों से मिलकर बनी होती है।
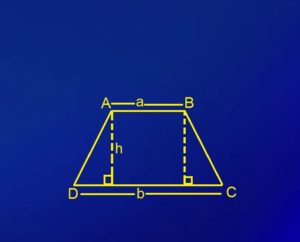
- ऊपर दी गयी आकृति में जैसा कि आप देख सकते हैं एक समलम्ब तीन आकृतियों से मिलकर बना होता है। ये आकृतियाँ दो त्रिभुज एवं एक आयत हैं। ये दो त्रिभुज समकोण त्रिभुज हैं जिनकी एक ही ऊंचाई h है।
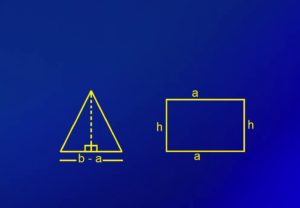
- जैसा कि हम ऊपर दी गयी आकृति में देख सकते हैं एक समलम्ब के दो भाग हो गये जिसका एक भाग दो त्रिभुजों से मिलाकर बनाया गया है एवं दूसरा भाग एक आयत है। अतः अब हमें क्षेत्रफल निकालने के लिए इन दो आकृतियों का क्षेत्रफल निकालना होगा।
त्रिभुज का क्षेत्रफल = 1/2 * आधार * ऊंचाई
आयत का क्षेत्रफल = लम्बाई * चौड़ाई
अतः समलम्ब का क्षेत्रफल = त्रिभुज का क्षेत्रफल + आयत का क्षेत्रफल
= b*h + 1/2*(b-a)* h
= h[b + 1/2*(b-a)]
= h [2b/2 + a-b/2]
= h(2b+a-b)/2
= h*(a+b)/2
इस लेख से सम्बंधित यदि आपका कोई भी सवाल या सुझाव है, तो आप उसे नीचे कमेंट में लिख सकते हैं।
गणित के अन्य लेख:
- बीजगणितीय सर्वसमिकाएँ क्या हैं?
- वर्ग का क्षेत्रफल
- ऊंचाई और दूरी
- भिन्न का जोड़
- भिन्न को घटाना
- नाव और धारा
- शंकु का छिन्नक
- बहुपद के शून्य और गुणनखंड कैसे निकालते हैं?
- पाइथागोरस प्रमेय
- शेषफल प्रमेय

Aayat ka kshetraphal equal to a*h hona chahiya
B*h ko replace karna hoga