चक्रीय चतुर्भुज के कोण, विकर्ण, सूत्र, परिभाषा, गुणधर्म एवं उदाहरण

चक्रीय चतुर्भुज की परिभाषा (meaning of cyclic quadrilateral in hindi)

चक्रीय चतुर्भुज एक ऐसा चतुर्भुज होता है जिसके चारों शिखर वृत्त की परिधि पर होते हैं। जैसा कि हम जानते हैं की एक चतुर्भुज कि चार भुजाएं होती हैं एवं इस चक्रीय चतुर्भुज में वे चारों भुजाएं एक वृत्त के अन्दर होती हैं एवं उनके शिखर इस वृत्त कि परिधि को छू रहे होते हैं।

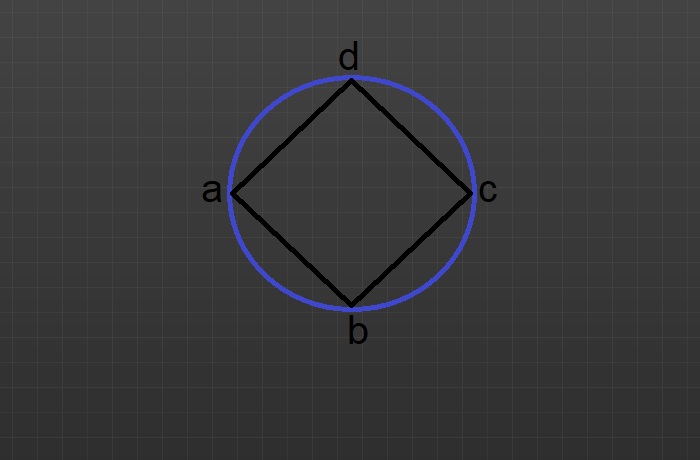
• जैसा कि आप ऊपर दिए गए चित्र में देख सकते हैं यहाँ हमारे पास एक वृत्त है एवं उसके अन्दर हमने एक चतुर्भुज बना रखा है। जैसा कि आप देख सकते हैं एक चतुर्भुज के चारों शिखर उस वृत्त की परिधि को छू रहे हैं अतः यह चतुर्भुज एक चक्रीय चतुर्भुज कहलायेगा।
• ऊपर वृत्त में जो चतुर्भुज है ज़रूरी नहीं है कि वैसा ही चतुर्भुज हो उसमे एक समचतुर्भुज भी हो सकता है या कोई और चतुर्भुज भी हो सकता है लेकिन जब तक उस चतुर्भुज के चारों शीर्ष उस वृत्त कि परिधि को छू रहे हैं जिसमे वो है तो वह चतुर्भुज चक्रीय चतुर्भज कहलायेगा।

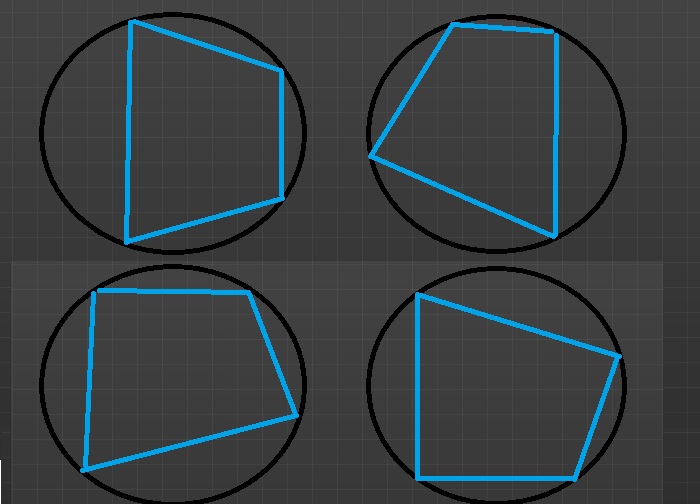
• ऊपर दिए गए चित्र में जैसा कि आप देख सकते हैं हमारे पास चार वृत्त एवं हर वृत्त में एक चतुर्भुज बना हुआ है। हम देख सकते हैं की चतुर्भुज में भुजाएं समान नहीं हैं लेकिन हर चतुर्भुज के चारों शीर्ष उस वृत्त की परिधि को छू रहे हैं जिससे वे चक्रीय चतुर्भुज कहलायेंगे।

ये भी पढ़ें:

• घन का आयतन क्या होता है?
• घन का क्षेत्रफल

चक्रीय चतुर्भुज का क्षेत्रफल (area of cyclic quadrilateral in hindi)

चक्रीय चतुर्भुज का क्षेत्रफल =

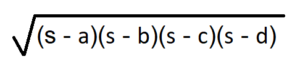
यहाँ,

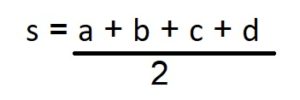
ये भी पढ़ें:

• बेलन का आयतन
• बेलन का क्षेत्रफल

चक्रीय चतुर्भुज के गुणधर्म (properties of cyclic quadrilateral in hindi)

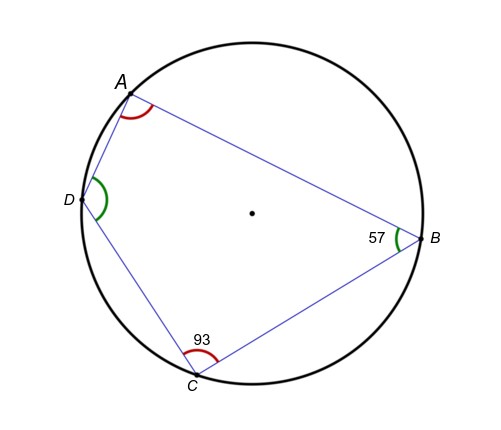
1. एक चक्रीय चतुर्भुज के विपरीत कोणों का जोड़ 180 अंश होता है। 

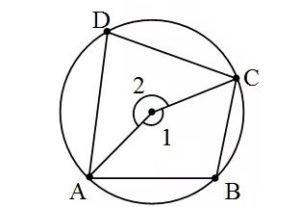
प्रमाण : कोण D  = ¹/₂ कोण 1 (परिधि पर कोण केंद्र के कोण का आधा होता है)

कोण B = ¹/₂ कोण 2 (परिधि पर कोण केंद्र के कोण का आधा होता है)

अतः कोण B + कोण D = ¹/₂ कोण (1 + 2) = ¹/_{2 *} (360)  =  180 अंश

2. एक चक्रीय चतुर्भुज के बाहरी कोण उसके भीतरी विपरीत कोण के बराबर होता हैं। 

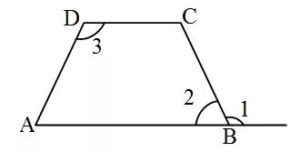
प्रमाण :  मान लिया ABCD एक चक्रीय चतुर्भुज है:

कोण 3 + कोण 2 = 180 अंश —1 (विपरीत कोणों का योग 180 अंश होता है)

इसी प्रकार, कोण 1 + कोण 2  = 180 अंश ——2

समीकरण 1 एवं 2 को जोड़ने पर :

कोण 3 + कोण 2 = कोण 1 + कोण 2  =  कोण  3 = कोण 1

इस प्रकार हम एक चक्रीय चतुर्भुज एक बाहरी कोण को भीतरी विपरीत कोण के बराबर सिद्ध करते हैं।

इस लेख से सम्बंधित यदि आपका कोई भी सवाल या सुझाव है, तो आप उसे नीचे कमेंट में लिख सकते हैं।

गणित के अन्य लेख:

• बीजगणितीय सर्वसमिकाएँ क्या हैं?
• वर्ग का क्षेत्रफल
• ऊंचाई और दूरी
• भिन्न का जोड़
• भिन्न को घटाना
• नाव और धारा
• शंकु का छिन्नक
• बहुपद के शून्य और गुणनखंड कैसे निकालते हैं?
• पाइथागोरस प्रमेय
• शेषफल प्रमेय