विषय-सूचि
द्विघात समीकरण की परिभाषा (quadratic equation)
ऐसा समीकरण जिसकी उच्चतम घात 2 होती है ऐसे समीकरण को द्विघात समीकरण कहा जाता है। द्विघात समीकरणों को हम दो घात वाला समीकरण भी कहा जाता है। इस समीकरण को एक उदाहरण के साथ समझते हैं।
मान लीजिये हमारे पास एक ज़मीन का टुकड़ा है एवं हम वहाँ एक घर बनाना चाहते हैं। मान लेते हैं ज़मीन का टुकड़ा 300 m2 है। अब हम अपने घर की चौड़ाई को अपनी लम्बाई को दो गुना रखना चाहते हैं।
उदाहरण :
हम यदि घर की लम्बाई को x मानते हैं तो घर की चौड़ाई 2x हो जायेगी। हम यह भी जानते हैं की घर का क्षेत्रफल लम्बाई x चौड़ाई होता है। तो हम इसे ऐसे लिख सकते हैं:
घर का क्षेत्रफल = (x)*(2x) = 2x2
2x2 = 300
x = 24.495 m
अतः जैसा कि आपने ऊपर देखा हम इस तरह द्विघात समीकरणों की मदद से वास्तविक जीवन की कई समस्याओं का आसान समाधान कर सकते हैं। द्विघात समीकरण हमें वास्तविक जीवन की समस्याओं को आसानी से समझने में मदद करता है।
द्विघात समीकरणों का मानक रूप
एक द्विघात समीकरण का मानक रूप ax2 + bx + c को माना जाता है। यहाँ x का मान अज्ञात होता है a, b एवं c गुणांक होते हैं एवं शून्य के बराबर नहीं होते है।
अतः
द्विघात समीकरण का मानक रूप : ax2 + bx + c
ये भी पढ़ें:
द्विघात समीकरणों को हल करने की विधि (solve quadratic equation)
द्विघात समीकरणों को हम दो विधियों से हल कर सकते हैं :
- गुणनखंड विधि
- पूर्ण वर्ग विधि
इससे पहले हमनें गुणनखंड विधि से द्विघात समीकरण को हल करना सीखा।
यहाँ हम पूर्ण वर्ग विधि से समीकरणों को हल करने की प्रक्रिया के बारे में जानेंगे।
पूर्ण वर्ग विधि (completing the square method in hindi)
जब हम एक द्विघात समीकरण जोकि ax2 + bx + c के रूप में होता है उसे हम जब a(x+h)2 + k के रूप में बदल देते हैं तब इस विधि को पूर्ण वर्ग बनाना कहते हैं।
आइये अब हम द्विपद समीकरण को हल करने की इस विधि की प्रक्रिया के बारे में पढ़ते हैं। इसे हमे के समीकरण के उदाहरण के साथ प्रक्रिया को समझेगे।
2x2 + x + 4 = 0
- ऊपर हम देख सकते हैं की हमें एक द्विपद समीकरण दिया गया है। इस समीकरण को हमें पूर्ण वर्ग विधि से हल करना है।
- सबसे पहले हमें यह देखना होता है की पहले पद का गुणांक 1 है या नहीं है। अगर गुणांक 1 से ज्यादा है तो हमें सभी पदों को पहले पद के गुणांक से भाग देना होगा।
- यहाँ इस समीकरण में जैसा की हम देख सकते हैं पहले पद का गुणांक 1 नहीं बल्कि 2 है तो हम तीनों पदों को 2 से भाग देंगे।
2×2/2+ x/2 + 4/2 = 0
x2 + x/2 + 2 = 0
- तो जैसा कि आपने देखा हमने 2 से सभी पदों को भाग कर दिया एवं अब हमारे पास एक नया समीकरण आगया है। अतः अब हम इसे आगे हल करेंगे।
- आगे हल करने के लिए हमें दुसरे पद के आधे भाग के वर्ग को इस समीकरण में जोड़ना एवं घटाना है l इस प्रकार:
दुसरे पद का आधा भाग : (1/2)/2 = 1/4
- हमें अब 1/4 के वर्ग को समीकरण में जोड़ना एवं घटाना है। तो चलिए यह करते हैं।
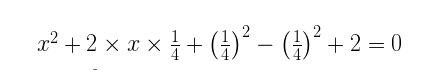
- तो जैसा की आपने देखा हमने दुसरे पद के आधे भाग के वर्ग को इस समीकरण में जोड़ दिया एवं घटा भी दिया। अब हम इसे आगे इस प्रकार हल करेंगे।
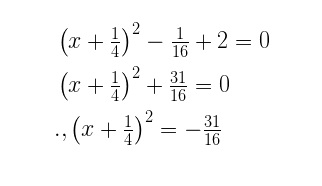
- इस प्रकार जैसा कि आप देख सकते हैं हमने एक समीकरण का हल कर दिया वो भी पूर्ण वर्ग की विधि से। अतः आप इस प्रकार समीकरणों का इस प्रकार सूत्र एवं प्रक्रिया का अनुसरण करके समीकरणों को हल कर सकते हैं।
इस लेख से सम्बंधित यदि आपका कोई भी सवाल या सुझाव है, तो आप उसे नीचे कमेंट में लिख सकते हैं।
गणित के अन्य लेख:
- बहुपद के शून्य और गुणनखंड कैसे निकालते हैं?
- शेषफल प्रमेय
- बीजगणितीय सर्वसमिकाएँ क्या हैं?
- वर्ग का क्षेत्रफल
- ऊंचाई और दूरी
- भिन्न का जोड़
- भिन्न को घटाना

Suparb