गोला: परिभाषा, गुणधर्म, आयतन एवं क्षेत्रफल

इससे पहले हमनें घन का आयतन और घन का क्षेत्रफल ज्ञात करने का तरीका जाना। इसके साथ घनाभ का आयतन और घनाभ का क्षेत्रफल ज्ञात करना भी पढ़ा।

गोले की परिभाषा (definition of sphere in hindi)

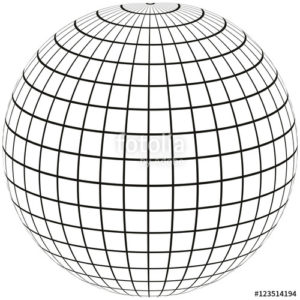
गोला एक विशेष प्रकार का ठोस होता है जिसका केवल एक तल होता है। यह ऐसा तल होता है जिसका हर बिंदु एक निश्चित बिंदु से समान दूरी पर होता है।

जिस प्रकार वृत्त एक द्विआयामी आकृति होती है उसी प्रकार गोला त्रिआयामी आकृति है जिसमे बहुत से बिंदु एक निश्चित बिंदु से सामान दूरी पर होते हैं।

गोले के गुणधर्म (properties of sphere in hindi)

• एक गोला पूर्णतया समरूप होता है।
• इसके तल पर सभी बिंदु इसके केंद्र से सामान दूरी पर होते हैं।

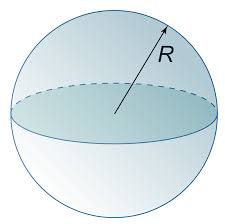
जैसा कि आप ऊपर दी गयी आकृति में देख सकते हैं यहाँ इस गोले पर बना हर बिंदु इसके केंद्र से सामान दूरी पर होता है।

• इसमें कोई शीर्ष या किनारा नहीं होता है।
• गोले का सिर्फ एक ही तल होता है।
• यह एक बहुतल आकृति नहीं होती है।

ये भी पढ़ें:

• चक्रीय चतुर्भुज के कोण, विकर्ण, सूत्र
• समलम्ब चतुर्भुज: क्षेत्रफल, परिभाषा, गुणधर्म, सूत्र

गोले का आयतन (volume of sphere in hindi)

जैसा कि हम जानते हैं आयतन से तात्पर्य होता है की वह त्रिआयामी ठोस अपने अन्दर कितनी क्षमता रखता है। इसका मतलब उसके अन्दर कितना द्रव्य आ सकता है। किसी ठोस के अन्दर कितना द्रव्य आ सकता है यह उसकी क्षमता की तरफ इशारा करता है।

लेकिन गोले का आयतन निकालने के लिए हम आर्कमिडीज का सिद्धांत प्रयोग करते हैं। इस सिद्धांत के अनुसार अगर हम किसी पानी से भरे बर्तन में कोई ठोस चीज़ डालते हैं तो बाहर गिरे पानी का आयतन उस ठोस के आयतन के बराबर होता है। लेकिन यह हर बार संभव नहीं होता है।

एक गोले का आयतन हम निचे दिए गए सूत्र में मान रखकर निकाल सकते हैं:

गोले का आयतन = 4/3 πr³

यहाँ r का तात्पर्य है उस दूरी से जो केंद्र एवं दुसरे हर बिंदु के बीच है। जैसा कि हम जानते हैं एक गोले के हर बिंदु से केंद्र के बीच में सामान दूरी होती है।

ये भी पढ़ें:

• बेलन का आयतन
• बेलन का क्षेत्रफल

गोले का पृष्ठ क्षेत्रफल (surface area of sphere in hindi)

गोले का एक विशेष तथ्य यह है कि उसका पूर्ण पृष्ठीय क्षेत्रफल एवं वक्र पृष्ठीय क्षेत्रफल अलग नहीं बल्कि एक ही होते हैं।एक गोले का क्षेत्रफल निकालने के लिए एक सिद्धांत है वह यह है की अगर हम एक गोले को एक धागे से लपेटे तो जितना धागा पूरे गोले को लपेतेगा उतना ही धागा उसी व्यास के चार वृत्तों को भरेगा।

इस सिद्धांत का प्रयोग करके हम एक गोले का पृष्ठ क्षेत्रफल निकाल सकते हैं।

अतः

गोले का क्षेत्रफल =  4 πr²

यहाँ r से तात्पर्य उस दूरी से है जो केंद्र एवं बाकी सभी बिंदु के बीच में है।

अब हम जानते हैं कीई एक गोले का पूर्ण एवं वक्र पृष्ठ क्षेत्रफल एक ही चीज़ होती है अतः अगर कभी हमें वक्र पृष्ठ निकालने के लिए कहा जाए तो हमें यही सूत्र लगाना है।

उदाहरण (solved examples and questions)

आइये अब हम गोले का क्षेत्रफल निकालना उदाहरणों के साथ सीखते हैं।

उदाहरण 1: एक गोले की त्रिज्या 3.2 cm है उस गोले का पृष्ठ क्षेत्रफल ज्ञात कीजिये।

हल:  हम सबसे पहले इस गोले कि त्रिज्या का माप लेंगे।

त्रिज्या : 3.2 cm 

अब हम गोले के पृष्ठीय क्षेत्रफल का सूत्र लगायेंगे।

गोले का पृष्ठीय क्षेत्रफल = 4π r² 
= 4π (3.2)²
= 4 × 3.14 × 3.2 × 3.2 
= 128.6 cm²

अतः एक गोला जिसकी त्रिज्या 3.2 cm है उसका पृष्ठीय क्षेत्रफल 128.6 cm² होगा।

अतः ऊपर दिए गए सूत्रों एवं प्रक्रियाओं से आप एक गोले का क्षेत्रफल एवं आयतन निकल सकते हैं।

इस लेख से सम्बंधित यदि आपका कोई भी सवाल या सुझाव है, तो आप उसे नीचे कमेंट में लिख सकते हैं।

गणित से सम्बंधित अन्य लेख:

• बीजगणितीय सर्वसमिकाएँ क्या हैं?
• वर्ग का क्षेत्रफल
• ऊंचाई और दूरी
• भिन्न का जोड़
• भिन्न को घटाना
• नाव और धारा
• शंकु का छिन्नक
• बहुपद के शून्य और गुणनखंड कैसे निकालते हैं?
• पाइथागोरस प्रमेय
• शेषफल प्रमेय