हीरोन का सूत्र: परिभाषा, सूत्र एवं उदाहरण

हीरोन के सूत्र की परिभाषा :

हीरोन का सूत्र (heron’s formula) ज्यामिति (geometry) में एक त्रिभुज का क्षेत्रफल ज्ञात करने में प्रयोग किया जाता है। अगर हमें एक त्रिभुज की तीन भुजाओं का माप ज्ञात है तो हम इस सूत्र का प्रयोग करके उस त्रिभुज का क्षेत्रफल ज्ञात कर सकते हैं।

जब हम इस सूत्र का प्रयोग करते हैं तो हमें उस त्रिभुज का क्षेत्रफल निकालने के लिए त्रिभुज के कोण ज्ञात करने की आवश्यकता नहीं होती तथा इससे यह बहुत ही आसान हो जाता है। इस सूत्र को प्रयोग करने के लिए हमारे पास बस तीनों भुजाओं का माप होना चाहिए एवं हम उस त्रिभुज का क्षेत्रफल ज्ञात कर सकते हैं।

जैसा कि आप ऊपर दी गयी आकृति में देख सकते हैं यहाँ एक त्रिभुज ABC दिया गया है। अगर हमें इसकी तीनों भुजाओं का माप ज्ञात है तो हम उसे हीरोन सूत्र में रखकर इस त्रिभुज का क्षेत्रफल ज्ञात कर सकते हैं।

हीरोन का सूत्र (heron’s formula in hindi)

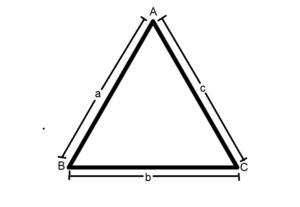
हीरोन के सूत्र के मुताबिक़ ऊपर दिए गए त्रिभुज की तीनों भुजा का माप सूत्र में रखने से इसका क्षेत्रफल आ जाएगा।

अर्ध परिमाप s = (a+b+c)/2

त्रिभुज का क्षेत्रफल = √[s(s-a)(s-b)(s-c)]

क्षेत्रफल निकालने की प्रक्रिया :

• एक त्रिभुज ABC जिसका हमें क्षेत्रफल निकालना है हमें सबसे पहले उसकी तीनों भुजाओं का माप चाहिए होता है। यह अक्सर सवाल में दिया होता है।
• तीनों भुजाओं का माप मिलने के बाद हमें इस त्रिभुज का अर्धपरिमाप निकालना होगा। अर्ध परिमाप को हम s से चिन्हित करते हैं। एक त्रिभुज का अर्ध परिमाप हम निम्न प्रकार से निकालते हैं :

s = (a+b+c)/2

• अर्ध परिमाप निकालने से हमारे पास s का मान आ जाता है। यही s का मान हमें आगे बचे सूत्र में रखना होगा। आगे का सूत्र निम्न है :

= √[s(s-a)(s-b)(s-c)]

• जब हम s का एवं भुजाओं का माप इस सूत्र में रखेंगें एवं आगे हल करेंगे तो आखिरी में हमारे पास इस त्रिभुज का क्षेत्रफल आ जाएगा।

उदाहरण:

आइये अब हम इस सूत्र से त्रिभुजों का क्षेत्रफल निकालना सीखते हैं :

उदाहरण 1: एक त्रिभुज की तीन भुजाओं का माप निम्न है : 3 cm, 4 cm एवं 5 cm इस त्रिभुज का क्षेत्रफल हीरोन के सूत्र से ज्ञात कीजिये।

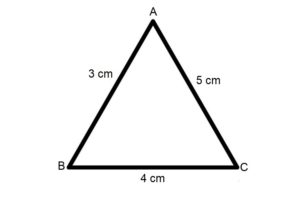
हल:  जैसा कि आप ऊपर देख सकते हैं यहाँ हमें एक त्रिभूज दिय गया है एवं हमें उसकी तीनों भुजाओं का माप पता है। अन हमें इस त्रिभुज का हीरोन के सूत्र से क्षेत्रफल ज्ञात करना है।

a = 3 cm, b = 4 cm एवं c = 5 cm

• सबसे पहले हम भुजाओं के माप से इस त्रिभुज का अर्ध परिमाप निकालेंगे।

s = (a+b+c)/2

s = (3 + 4 +5) / 2 

s = 12/2 = 6 cm

s = 6 cm

• अब जैसा कि आप देख सकते हैं हमें इस त्रिभुज का अर्ध परिमाप मिल गया है तो अब हम आगे बढ़ते हैं एवं अब सूत्र में अर्ध परिमाप का मान रखकर आगे इस त्रिभुज का क्षेत्रफल निकालते हैं।

त्रिभुज का क्षेत्रफल = √[s(s-a)(s-b)(s-c)]

= √6(6-3)(6-4)(6-5)

=√6x3x2x1

=√36

=6

अतः एक त्रिभुज जिसकी तीन भुजाएं क्रमश 3, 4 एवं 5 cm हैं उसका क्षेत्रफल 6 cm होगा।

जैसा कि आपने देखा हमने हीरोन का सूत्र का प्रयोग करके एवं इस प्रक्रिया का अनुसरण करके एक त्रिभुज का क्षेत्रफल निकाल दिया। इसी प्रकार हम और त्रिभुज के भी क्षेत्रफल निकाल सकते हैं। इसकी बस यही शर्त है कि हमें दिए गए त्रिभुज की तीनों भुजाओं का माप ज्ञात होना चाहिए।

इस लेख से सम्बंधित यदि आपका कोई भी सवाल या सुझाव है, तो आप उसे नीचे कमेंट में लिख सकते हैं।

गणित से सम्बंधित अन्य लेख:

• बीजगणितीय सर्वसमिकाएँ क्या हैं?
• वर्ग का क्षेत्रफल
• ऊंचाई और दूरी
• भिन्न का जोड़
• भिन्न को घटाना
• नाव और धारा
• शंकु का छिन्नक
• बहुपद के शून्य और गुणनखंड कैसे निकालते हैं?
• पाइथागोरस प्रमेय
• शेषफल प्रमेय