शंकु का छिन्नक : परिभाषा, गुणधर्म, क्षेत्रफल एवं आयतन

छिन्नक क्या होता है? (frustum of cone in hindi)

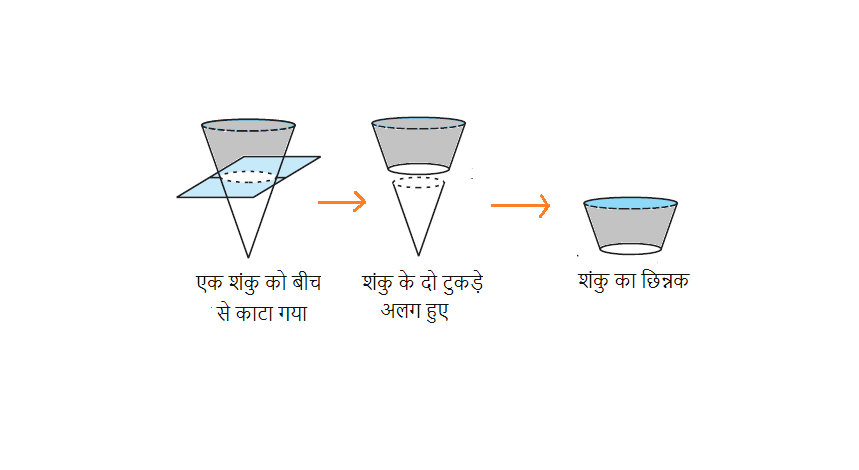
एक सम परिपत्र(right circular) शंकू को नोक कि तरफ से थोडा काट देने पर जो त्रिआयामी आकृति बनती है उसे हम उस शंकु का छिन्नक कहते है। ऐसे काटने पर जो आकृति बनती है उस आकृति के ऊपर एवं नीचे वृत्त होते हैं एवं दोनों वृत्त समान्तर होते हैं एवं उनका केंद्र समान होता है।

जैसा की आप ऊपर दिए गए चित्र में देख सकते हैं यहाँ हमारे पास एक सैम परिपत्र शंकु है एवं हमने इसे दो हिस्सों में काट दिया। इस शंकु का बिना नोक वाला हिस्सा इस शंकु का छिन्नक होगा इसमें दोनों और वृत्त हैं एवं ये समांतर हैं।

ये भी पढ़ें:

• घन का आयतन क्या होता है?
• घन का क्षेत्रफल

छिन्नक के गुणधर्म (formulas of frustum of cone)

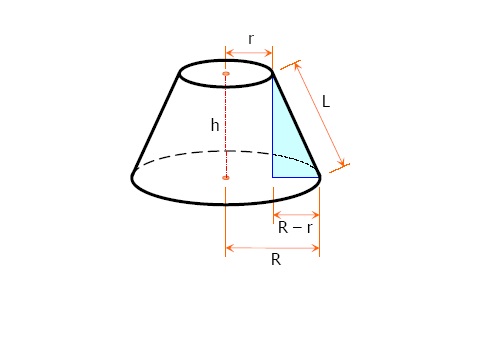
• एक छिन्नक के दो गोलाकार आधारों के बीच जो ऊंचाई होती है वह वृत्तों के बीच समलम्ब दूरी होती है। यह दूरी दोनों वृत्तों के केंद्र को एक दुसरे से जोडती है एवं ये दोनों वृत्त दिखने में समान एवं गुण में समान्तर होते हैं।
• जैसा की आप ऊपर दिए गए चित्र में देख सकते हैं यहाँ दोनों वृत्तों के बीच जो लांब दूरी है उसे h से दर्शाया गया है एवं यहाँ दोनों वृत्तों के केन्द्रों को जोड़ रही है।
• ये दोनों वृत्त एक दुसरे से हर बिंदु से समान्तर हैं एवम इनके केंद्र एक रेखा खंड से जुड़ रहे हैं जिसे h नाम दिया गया है।
• इस छिन्नक की तिर्यक ऊंचाई को l से चित्रित किया जाता है एवं यह दोनों वृत्त की परिधियों को जोडती है।
• बड़े वृत्त की त्रिज्या को हम R नाम देते हैं एवं छोटे वृत्त की त्रिज्या को हम r नाम देते हैं। ऐसा इसलिए ताकि हम इन्हें अलग अलग पहचान सके।

ये भी पढ़ें:

• भिन्न को गुना करना
• भिन्न का भाग कैसे करें?

छिन्नक का आयतन (perimeter of frustum of cone)

जैसा की हमने पहले बताया की छिन्नक एक शंकु का कटा हुआ हिस्सा होता है इसलिए हमें एक छिन्नक का आयतन निकालने के लिए दो सम परिपत्र शंकुओं का आयतन निकलना पड़ेगा। हम यह इस प्रकार करेंगे :

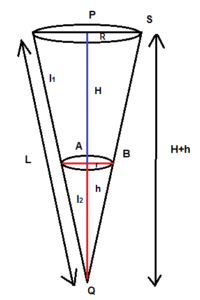
• ऊपर दिए गए चित्र में जैसा की हम देख देख सकते हैं:

पूरे शंकु की ऊंचाई: H+h

एवं कुल तिर्यक ऊंचाई =  l1+ l2 

पूरे शंकु की त्रिज्या : R

एवं नीचे कटे हुए शंकु की त्रिज्या : r

• ऊपर दिए गए माप के आधार पर :

पूरे शंकु का आयतन : 1/3 π R² H’ = 1/3 π R² (H+h) 

छोटे शंकु का आयतन  :  1/3 πr²h

• अब हमें इस छिन्नक का आयतन निकालने के लिए पूरे शंकु के आयतन में से छोटे शंकु के आयतन को घटाना होगा इससे हमें इस छिन्नक का आयतन मिल जाएगा।
• हम यह इस प्रकार करेंगे :

= 1/3 πR²H’ -1/3 πr²h
= 1/3 πR²(H+h) -1/3 πr²h
=1/3 π[R² (H+h)-r² h]

• जैसा कि हम चित्र में देख सकते हैं : R/ r = H+h / h ⇒ H+h = Rh/r अतः इनका माप रखने पर :

=1/3 π [ R² (Rh/r)-r² h ] =1/3 π  [R³h/r-r² h )]
=1/3 π h (R³/r-r² )  =1/3 π h (R³-r³ / r)

अतः हमारे पास एक चिन्नक का आयतन निकालने का सूत्र आ गया है वह है :

शंकु के छिन्नक का आयतन : 1/3 π h [(R³-r³)/ r]

छिन्नक का क्षेत्रफल (area of frustum of cone)

जिस प्रकार हमने इस छिन्नक का आयतन निकाला था उसी प्रकार छिन्नक का पृष्ठ क्षेत्रफल निकलेगा। हमें बस पूरे शंकु का क्षेत्रफल निकालना है एवं उसमें से छोटे शंकु का क्षेत्रफल को घटा देना है। ऐसा करने पर जो उत्तर आएगा वही उस छिन्नक का क्षेत्रफल होगा।

यदि उसमें एक वृत्त का क्षेत्रफल और जोड़ देंगे तो वह पूर्ण पृष्ठीय क्षेत्रफल बन जाएगा एवं अगर दोनों वृत्त का क्षेत्रफल घटा देंगे तो वह वक्र प्रष्ठिया क्षेत्रफल बन जाएगा।

अतः

छिन्नक का पूर्ण पृष्ठीय क्षेत्रफल : π l₁ (R+r) +πR² +πr²

छिन्नक का वक्र पृष्ठीय क्षेत्रफल : π(R+r)l₁

अगर किसी में हमें इस शंकु एवं छिन्नक की तिर्यक ऊंचाई नहीं दे रखी है तो हम उसे इस प्रकार निकाल सकते हैं :

= √[H² +(R-r)²]

अतः ऊपर दिए गए सूत्रों से आप एक छिन्नक का आयतन, क्षेत्रफल एवं तिर्यक ऊंचाई निकाल सकते है।

इस लेख से सम्बंधित यदि आपका कोई भी सवाल या सुझाव है, तो आप उसे नीचे कमेंट में लिख सकते हैं।

गणित के अन्य लेख:

• बहुपद के शून्य और गुणनखंड कैसे निकालते हैं?
• शेषफल प्रमेय
• बीजगणितीय सर्वसमिकाएँ क्या हैं?
• वर्ग का क्षेत्रफल
• ऊंचाई और दूरी
• भिन्न का जोड़
• भिन्न को घटाना
• नाव और धारा