वृत्त का वृत्तखंड: क्षेत्रफल, परिभाषा, सूत्र एवं उदाहरण

पिछले लेख में हमनें जाना त्रिज्यखंड क्या होता है? इस लेख में हम त्रिज्यखंड के बारे में पढेंगे।

वृत्तखंड की परिभाषा (segment of circle definition in hindi)

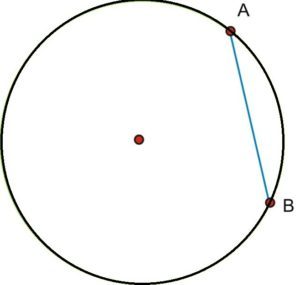
वृत्तखंड एक वृत्त (circle) का वह हिस्सा होता है जो एक जीवा एवं चाप के बीच में घिरा हुआ होता है। अगर हम एक त्रिज्यखंड को लेकर उसके उन बिन्दुओं को मिला दे जो परिधि को छूते हैं तो हमें एक वृत्तखंड मिल जाएगा।

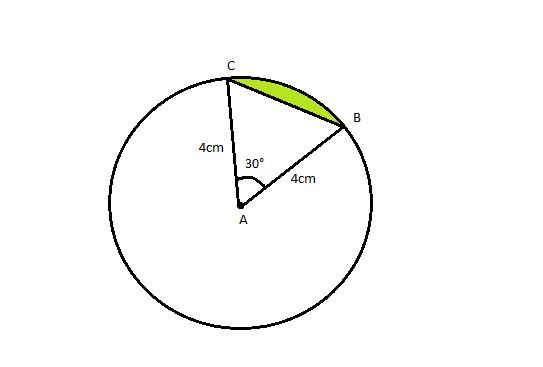
जैसा कि आप ऊपर दिए आगे चित्र में देख सकते हैं यहाँ हमें यहाँ हमें एक वृत्त दे रखा है एवं उसमे एक जीवा दे रखी है यह जीवा इस वृत्त की परिधि को दो बिन्दुओं पर छू रही है। जैसा की आप देख सकते हैं यहाँ यह जीवा परिधि के दो बिन्दुओं को छूकर एक वृत्तखंड बना रही है। जो दो बिन्दुओं को यह जीवा छू रही है उन्हें A एवं B बिंदु नाम देंगे।

वृत्तखंड का क्षेत्रफल (area of segment of circle in hindi)

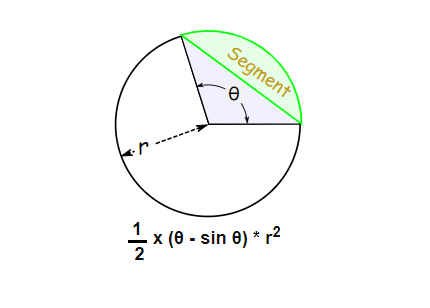
• जैसा की आप ऊपर दिए गए चित्र में देख सकते हैं यहाँ हमें एक वृत्त दिया गया है उसके नीचे हमें उस वृत्त के वृत्तखंड का क्षेत्रफल दिया गया है।
• हम देख सकते हैं यहाँ :

वृत्त का वृत्तखंड = त्रिज्यखंड का क्षेत्रफल – त्रिभुज का क्षेत्रफल 

उदाहरण (examples)

आइये एक वृत्तखंड का क्षेत्रफल निकालना हम एक उदाहरण के साथ सीखते हैं :

उदाहरण : एक वृत्ताकार मैदान के चारों और समान चौड़ाई की पक्की सड़क बनी हुई है। यदि मैदान की त्रिज्या 20 cm है इसमें मैदान तथा सड़क का क्षेत्रफल समान है तो सड़क की चौड़ाई ज्ञात कीजिये।

हल : माना सड़क की चौड़ाई x मीटर है।

दिया है :

मैदान का क्षेत्रफल = सड़क का क्षेत्रफल 

जैसा की आप देख सकते हैं यहाँ मैदान एवं सड़क का क्षेत्रफल समान है अतः हम उन्हें एक समीकरण में समान रखके एवं उनके सूत्र में मान रखकर दोनों को ज्ञात करेंगे।

अतः

मैदान का क्षेत्रफल  = 1/2 * (सड़क + मैदान) का क्षेत्रफल

अर्थात:

 मैदान का क्षेत्रफल = 1/2 π (20 + x)² वर्ग cm

किन्तु

मैदान का क्षेत्रफल = p * 20² वर्ग cm

अथवा

(20 + x)² = 2 x 20²

20 + x = 20√2

x = 20(√2 – 1)

x = 20(1.414 – 1) 

x = 20 x 0.414

x = 8.28 cm

अतः सड़क की चौड़ाई = 8.28 cm

इस लेख से सम्बंधित यदि आपका कोई भी सवाल या सुझाव है, तो आप उसे नीचे कमेंट में लिख सकते हैं।

गणित से सम्बंधित अन्य लेख:

• बीजगणितीय सर्वसमिकाएँ क्या हैं?
• वर्ग का क्षेत्रफल
• ऊंचाई और दूरी
• भिन्न का जोड़
• भिन्न को घटाना
• नाव और धारा
• शंकु का छिन्नक
• बहुपद के शून्य और गुणनखंड कैसे निकालते हैं?
• पाइथागोरस प्रमेय
• शेषफल प्रमेय