विषय-सूचि
इससे पहले हमनें माध्यिका, माध्य एवं बहुलक (mean, median, mode) के बारे में पढ़ा।
माध्य क्या होता है? (mean in hindi)

जिस प्रकार माध्यिका (median) अंकों के समूह के बीच में आती है, अंकगणित माध्य दी गयी संख्याओं के औसत के समान है। यह एक संख्याओं के समूह में से वह संख्या है जो उन सभी संख्याओं का प्रतिनिधित्व करती है।
हम मान लेते हैं की हमें एक संख्याओं का निश्चित समूह दे रखा है और हमें इस संख्याओं के समूह का माध्य निकालना है तो हमें बस इन संख्याओं को जोड़ना है एवं ये जितनी संख्याएं हैं उस संख्या को इन सभी संख्याओं के योग से भाग दे देना है। इससे हमें इस संख्याओं के समूह का माध्य पता चल जाएगा। अतः इस दी गयी प्रक्रिया से हम संख्याओं के समूह का माध्य निकालते है।
माध्य का सूत्र (formula to find mean):

जैसा की आप सूत्र में देख सकते हैं की हमें जितनी भी संख्या दे रही हैं हमें उनका योग कर देना है एवं हमें यह भी गिना है कि वे कितनी संख्याएं हैं। अब हमें संख्याओं के योग को उनके तादाद से भाग दे देना है। ऐसा करने से हमारे पास जो संख्या आएगी वह संख्या माध्य कहलाएगी।
उदाहरण :
आइये इसे हम एक उदाहरण के साथ समझते हैं :
एक परिवार में दो भाई हैं। उन दोनों भाइयों की अलग-अलग ऊंचाई है। छोटे भाई की ऊंचाई 128 cm है जबकि उसके बड़े भाई की ऊंचाई 150 cm है। अब उनके माता पिता उन दोनों भाइयों की औसत ऊंचाई जानना चाहते हैं। ऐसा करने के लिए उन्हें उन दोनों भाइयों की ऊंचाई का माध्य निकालन होगा जिससे उनकी औसत ऊंचाई निकल आएगी।
= (128+150)/2
= 278/2
= 139 cm
अतः हमने दोनों की ऊंचाइयों को जोड़ा एवं उन्हें 2 से भाग दे दिया एवं ऐसा करने से उनकी औसत ऊंचाई एवं उनकी ऊंचाई का माध्य निकल आया।
ये भी पढ़ें:
आंकड़ों के समूह का माध्य कैसे निकालते हैं? (arithmetic mean formula in hindi)
अभी तक हमने देखा की हम साधारण माध्य कैसे निकालते हैं लेकिन अब हम सीखेंगे की आंकड़ों के समूह का माध्य कैसे निकालते हैं।
| वर्ग अंतराल | आवृति |
|---|---|
| 51 – 55 | 2 |
| 56 – 60 | 7 |
| 61 – 65 | 8 |
| 66 – 70 | 4 |
- ऊपर जैसा की आप देख सकते हैं हमारे पास एक सारणी है जिसमे विभिन्न आंकड़ों का समूह है। यहाँ (51-55, 56-60, आदि) वर्ग अंतराल हैं एवं इनमें 5 का अंतराल है। इन सभी वर्गों के मध्य बिंदु 53, 58, 63 and 68 हैं।
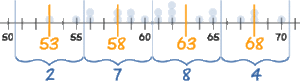
- जैसा की आपने देखा हमने सभी वर्ग अंतरालों के मध्य बिंदु ज्ञात कर लिए अब हम उन मध्य बिन्दुओं से एक और सारणी बनायेंगे।
| मध्यबिंदु | आवृति |
|---|---|
| 53 | 2 |
| 58 | 7 |
| 63 | 8 |
| 68 | 4 |
- ऊपर आपने देखा हमने पहली वाली सारणी के वर्ग अंतरालों के मध्य बिन्दुओं से एक और सारणी बना ली है। अब हम इस सारणी से मध्य बिंदु की गणना करेंगे। हम उस सारणी में मध्य बिन्दुओं को आवृति से गुना करेंगे एवं एक और स्तम्भ बनाकर उसमे लिखेंगे।
| मध्यबिंदु x |
आवृति f |
मध्यबिंदु × आवृति fx |
|---|---|---|
| 53 | 2 | 106 |
| 58 | 7 | 406 |
| 63 | 8 | 504 |
| 68 | 4 | 272 |
| कुल: | 21 | 1288 |
- अतः इसका माध्य होगा :
1288 / 21 = 61.333
अतः इस प्रकार हम आंकड़ों के समूह का माध्य निकाल सकते हैं।
इस लेख से सम्बंधित यदि आपका कोई भी सवाल या सुझाव है, तो आप उसे नीचे कमेंट में लिख सकते हैं।
गणित के अन्य लेख:
- पाइथागोरस प्रमेय
- शेषफल प्रमेय
- बीजगणितीय सर्वसमिकाएँ क्या हैं?
- वर्ग का क्षेत्रफल
- ऊंचाई और दूरी
- भिन्न का जोड़
- भिन्न को घटाना
- नाव और धारा
- शंकु का छिन्नक
- बहुपद के शून्य और गुणनखंड कैसे निकालते हैं?


Sir aap formula English Se bhi likh Diya kare
Nhi hindi me shi h
Sir aapko buhut experience hai sir
5 प्रेक्षणों का माध्य है 145 परिकलित किया जाता है परंतु बाद में यह पाया जाता है कि एक आंकड़े को गलती से 25 की जगह 45 पढ़ लिया जाता है तो प्रेक्षणों का माध्य ज्ञात कीजिए।
141
41
iske gud or dosh
Labh or hani btayiye