विषय-सूचि
बेज प्रमेय की परिभाषा (bayes theorem in hindi)
बेज प्रमेय किसी एक घटना की संभावना का उपयोग कर एक नई घटना की पूर्व संभावना की गणना करने में सहायता करती है।
इसे हम कुछ इस प्रकार समझ सकते हैं की हमारे पास तीन थैले हैं एवं वे लाल एवं काली गेंदों से भरे पड़े हैं। हम इन थैलों में से किसी भी रंग की गेंद निकालने की घटना की संभावना की गणना कर सकते हैं। इसके साथ ही हम इन तीन थैलों में से एक थैले को चुनने की संभावना निकाल सकते हैं।
लेकिन हमारे पास तीन थैले हैं एवं हमें उनमें से एक को चुनकर उसमें से काली गेंद निकालने की संभावना निकालनी है तो यह थोड़ा पेचीदा हो जाता है। अतः इसकी गणना करने के लिए हमारे पास बेज की प्रमेय है एवं इस प्रमेय में एक सूत्र है जिससे हमें इसे गणना करने में आसानी होती है।
ये भी पढ़ें:
उदाहरण (bayes theorem probability in hindi)
आइये अब हम उदाहरण के तौर पर एक घटना लेते हैं :
मान लीजिये एक बच्चे के पास फलों के तीन थैले हैं जिनमे से पहले थैले में 5 सेब एवं 3 संतरे हैं। दुसरे थैले में 3 सेब एवं 6 संतरे एवं तीसरे थैले में 2 सेब एवं तीन संतरे हैं। इन तीनों में से किसी एक थैले में से कोई एक फल निकाला जाता है। यह एक सेब निकलता है। ऐसी घटना की संभावना ज्ञात कीजिये की यह सेब तीसरे थैले में से निकाला गया था।
हल : हम तीनों थैलों को चुनने की प्रायिकता लेते हैं:
p(E1)= P(E2) = P(E3) = 1⁄3
पहले थैले में से एक सेब निकलने की प्रायिकता है :
P(A | E1) = 5⁄8
दुसरे थैले में से एक सेब निकलने की प्रायिकता है :
P(A|E2) = 3⁄9 = 1⁄3
एवं तीसरे थैले में से एक सेब निकलने की प्रायिकता है:
P(A | E3) = 2⁄5
अब हमें एक सेब निकालने की प्रायिकता निकालनी है जब हमें दे रखा है कि सेब तीसरे थैले में से निकला है। इसे गणना करने में हमें बेज का सूत्र मदद करेगा जोकि है :
P(E3| A) = [P(E3). P(A | E3)] ÷ [P(E1)×P(A |E1) + P(E2)×P(A | E2) + P(E3)×P(A|E3)]
अब हम इस सूत्र में सभी मान रख देंगे एवं इसे हल करदेंगे जिससे हमारी सेब की प्रायिकता निकल आएगी।
P(E3| A) 0= 1⁄3 × 2⁄5 ÷ [(1⁄3 × 5⁄8) + (1⁄3 × 3⁄9) + (1⁄3 × 2⁄5)]
= (2⁄15) ÷ (163⁄360)
= 48⁄163
इस लेख से सम्बंधित यदि आपका कोई भी सवाल या सुझाव है, तो आप उसे नीचे कमेंट में लिख सकते हैं।
गणित के अन्य लेख:
- बहुपद के शून्य और गुणनखंड कैसे निकालते हैं?
- शेषफल प्रमेय
- बीजगणितीय सर्वसमिकाएँ क्या हैं?
- वर्ग का क्षेत्रफल
- ऊंचाई और दूरी
- भिन्न का जोड़
- भिन्न को घटाना
- नाव और धारा

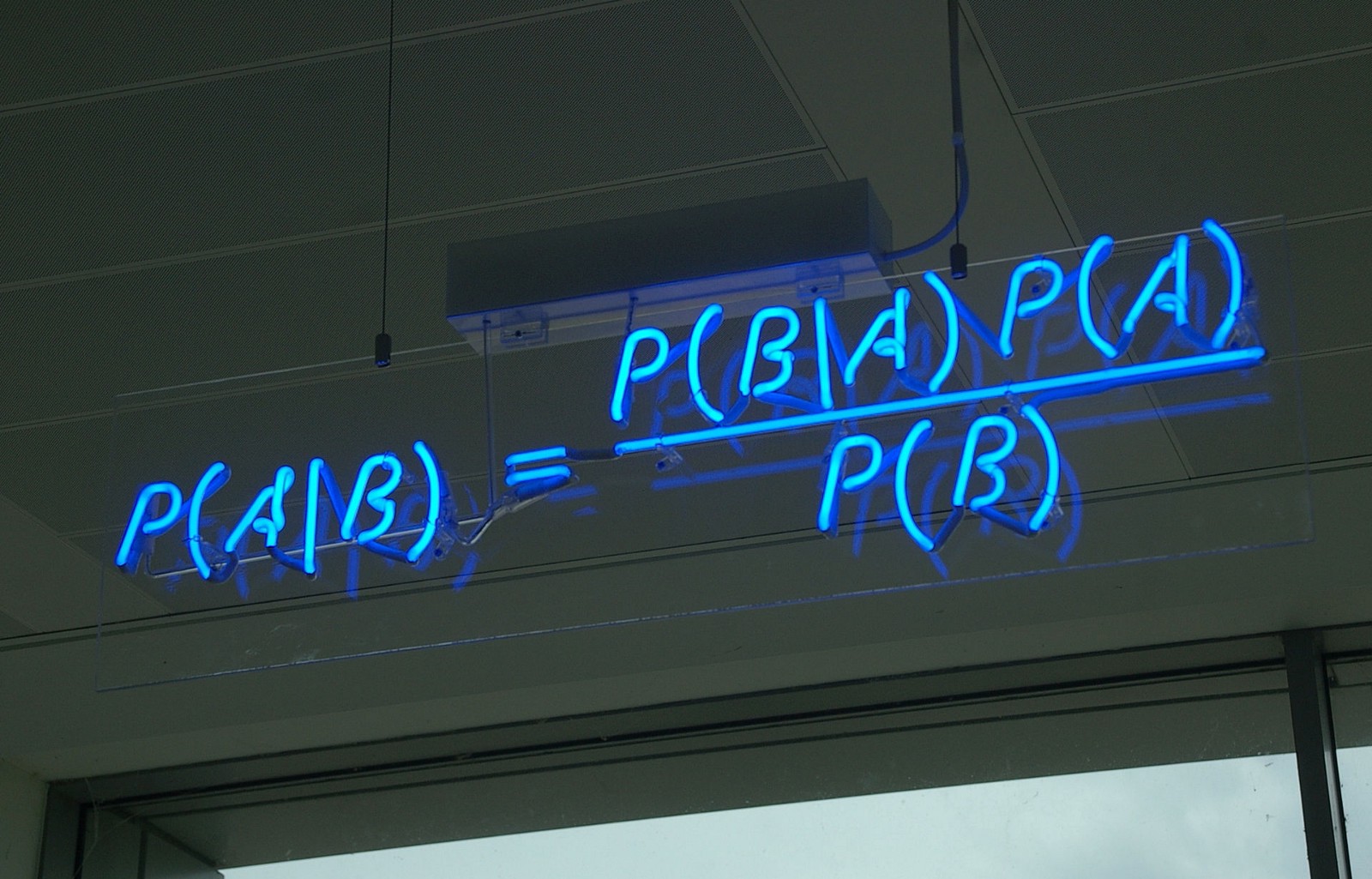
P(E3| A) = [P(E3). P(A | E3)] ÷ [P(E1)×P(A |E1) + P(E2)×P(A | E2) + P(E3)×P(A|E3)] esko smjha djiye please mera paper hai kl ye formula nhi aaya smjh me esme E and P kya hai