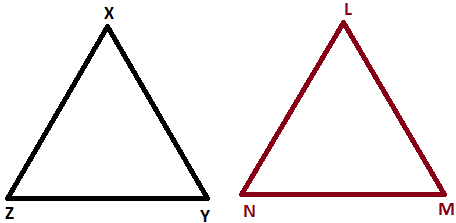विषय-सूचि
सर्वांगसमता क्या होती है? (congruent triangles in hindi)
जब दो त्रिभुज की सारी भुजाओं एवं कोणों का माप समान होता है तो वे त्रिभुज सर्वांग्सम होते हैं। जब ऐसा होता है तो एक त्रिभुज को दूसरे त्रिभुज पर अध्यारोपित करने पर पहला त्रिभुज दूसरे त्रिभुज को पूर्णतया ढक लेता है।

ऊपर दी गयी आकृतियों में जैसा कि हम देख सकते हैं यहाँ हमें दो त्रिभुज दे रखे हैं। ये दो त्रिभुज बिलकुल समान हैं। अगर हम इन्हें एक के ऊपर एक रख्नेगे तो फिर एक त्रिभुज दुसरे त्रिभुज को पूरी तरह ढक लेगा।
जो त्रिभुज सर्वांग्सम होते हैं वे चाहे दोनों चाहे एक समान स्थिति में ना हों लेकिन वे फिर भी सर्वांग्सम ही होंगे। जैसे:
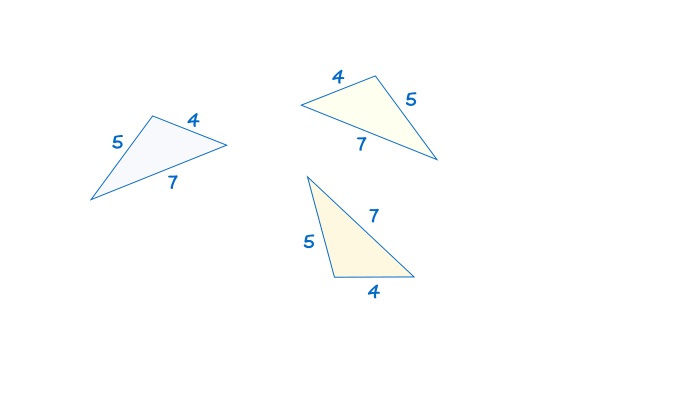
- जैसा कि आप ऊपर दी गयी आकृतियों में देख सकते हैं यहाँ हमें तीन त्रिभुज दे रखे हैं जिनकी तीनों भुजाएं समान माप कि हैं लेकिन उनकी स्थिति अलग अलग है। स्थिति अलग होने के बावजूद भी वे तीनों त्रिभज एक दुसरे के सर्वांग्सम होंगे। सर्वांग्सम होने के लिए बस उनकी भुजा एवं कोण समान होने चाहिए उनकी स्थिति चाहे कैसी भी हो इससे कोई फर्क नहीं पड़ता है।
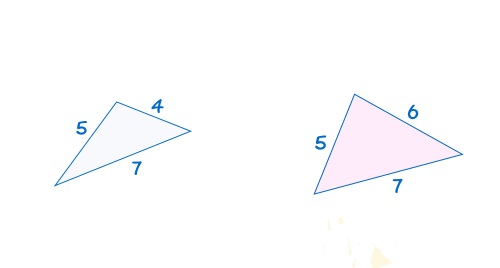
- ऊपर जैसा कि आप देख सकते हैं यहाँ दो त्रिभुज हैं जिनकी स्थिति एक समान है लेकिन इनकी भुजाओं का माप समान नही है। इन त्रिभुजों की भुजाओं का माप भिन्न भिन्न है। अतः ये त्रिभुज सर्वांग्सम नहीं होंगे।
ये भी पढ़ें:
त्रिभुजों की सर्वांगसमता के नियम (rules of congruent triangles in hindi)
भुजा-कोण-भुजा सर्वांगसमता (side angle side theorem in hindi)
जैसा की इस नियम के नाम से ही प्रतीत हो रहा है, इसके अनुसार दो त्रिभुज सर्वांग्सम होंगें जब एक त्रिभुज की दो भुजाएं एवं उनका अंतरकोण क्रमशः दुसरे त्रिभुज की दो भुजाओं एवं अंतरकोण के बराबर हो।
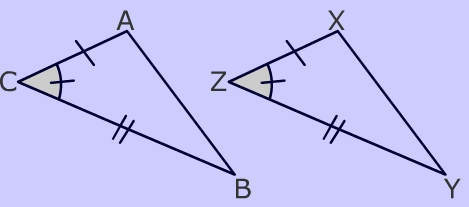
जैसा की आप ऊपर दिए गए दो त्रिभुजों में देख सकते हैं :
AC = XZ
कोण C = कोण Z
CB = ZY
इस तरह त्रिभुज ABC एवं त्रिभुज XYZ भुजा कोण भुजा नियम से सर्वांग्सम हो जाते हैं।
2. कोण-भुजा-कोण नियम (angle side angle congruence in hindi)
जैसा की इस नियम के नाम से ही प्रतीत हो रहा है दो त्रिभुज सर्वांग्सम हो जायेंगे यदि एक त्रिभुज के दो कोण तथा उनके अंतर्गत भुजा दूसरे त्रिभुज के क्रमशः दो संगत कोणों और उनकी अन्तर्गत भुजा के बराबर होती है। निचे दी गयी आकृति को देखें :
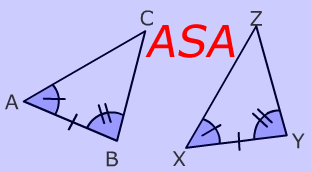
जैसा की आप ऊपर दिए गए दो त्रिभुजों में देख सकते हैं :
कोण A = कोण x
AB = XY
कोण B = कोण Y
इस तरह से त्रिभुज ABC एवं XYZ कोण-भुजा-कोण के नियम से सर्वांग्सम हो गए हैं।
3. भुजा-भुजा-भुजा नियम (side side side congruence in hindi)
जैसा की इस नियम के नाम से ही प्रतीत हो रहा है की दो त्रिभुज सर्वांग्स्म हो जायेंगे यदि एक त्रिभुज की तीन भुजाएँ दूसरे त्रिभुज की क्रमशः तीनों संगत भुजाओं के बराबर होती हैं। इसमें हमें कोण से कोई मतलब नहीं है बस त्रिभुजों कि भुजाएं समान होनी चाहिए। निचे दी गयी आकृति को देखें :
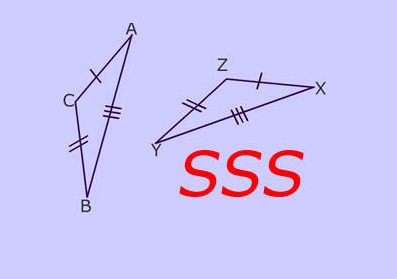
जैसा की आप ऊपर दिए गए दो त्रिभुजों में देख सकते हैं की :
AC = ZX
CB = ZY
AB = YX
जैसा की आपने देखा इन दोनों त्रिभुजों में तीनों की तीनों भुजाएं सामान हो गयी हैं जिससे ये त्रिभुज भुजा भुजा भुजा के नियम से एक दुसरे से सर्वांग्स्म हो गए हैं।
4. कोण-कोण-भुजा नियम (angle angle side congruence in hindi)
जैसा की इस नियम के नाम से ही प्रतीत हो रहा है की दो त्रिभुज सर्वांग्स्म हो जायेंगे यदि एक त्रिभुज के दो कोण और इन कोणों के अन्तर्गत भुजा के अतिरिक्त कोई एक भुजा दूसरे त्रिभुज के क्रमशः संगत कोणों और संगत भुजा के बराबर होती है।
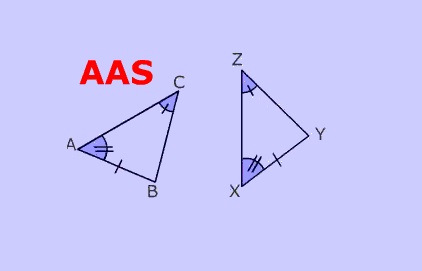
कोण A = कोण X
कोण C = कोण Z
AB = XY
जैसा की आप ऊपर दिए गए त्रिभुजों में देख सकते हैं की ये दोनों त्रिभुज कोण कोण भुजा नियम से एक दुसरे के सर्वांग्स्म हो गए हैं क्योंकि दो कोण और इन कोणों के अन्तर्गत भुजा के अतिरिक्त कोई एक भुजा दूसरे त्रिभुज के क्रमशः संगत कोणों और संगत भुजा के बराबर हो गयी है।
5. समकोण-कर्ण-भुजा नियम (right angle side congruence in hindi)
जैसा की इस नियम के नाम से ही प्रतीत हो रहा है दो त्रिभुज सर्वांग्स्म हो जायेंगे यदि एक त्रिभुज का कर्ण और एक भुजा दूसरे समकोण त्रिभुज के क्रमशः कर्ण और संगत भुजा के बराबर होता है। यह नियम सिर्फ समकोण वाले त्रिभुजों में ही कारगर होता है।
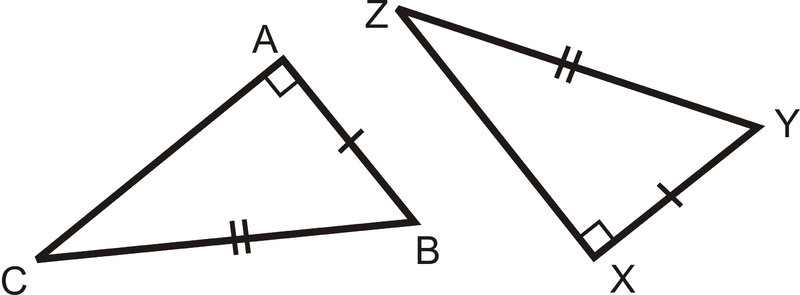
जैसा की आप ऊपर दिए गए त्रिभुजों में देख सकते हैं की :
कोण A = कोण X
AB = XY
CB = ZY
जैसा कि आपने देखा ऊपर दिए गए दो त्रिभुज में समकोण व दो भुजाओं के समान होने से वे समकोण कर्ण भुजा के नियम से सर्वांग्सम हो गए है।
इस लेख से सम्बंधित यदि आपका कोई भी सवाल या सुझाव है, तो आप उसे नीचे कमेंट में लिख सकते हैं।
गणित के अन्य लेख:
- बीजगणितीय सर्वसमिकाएँ क्या हैं?
- वर्ग का क्षेत्रफल
- ऊंचाई और दूरी
- भिन्न का जोड़
- भिन्न को घटाना
- नाव और धारा
- शंकु का छिन्नक
- बहुपद के शून्य और गुणनखंड कैसे निकालते हैं?
- पाइथागोरस प्रमेय
- शेषफल प्रमेय