घन और घनाभ में अंतर

घन क्या होता है ?

घन (cube) एक ऐसी त्रिआयामी आकृति को कहा जाता है जिसकी लम्बाई, चौड़ाई एवं ऊँचाई सामान होती हैं। एक घन में छः फलक, बारह किनारे एवं आठ कोने होते हैं।

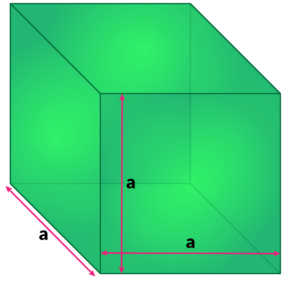
जैसा कि आप ऊपर दी गयी आकृति में देख सकते हैं यहाँ एक त्रिआयामी आकृति दी गयी है जिसकी लम्बाई, चौड़ाई एवं ऊंचाई एक सामान है। ऐसा होने से ये एक घन कहलायेगा।

घन के गुणधर्म (properties of cube in hindi)

शीर्ष (vertices) : शीर्ष वह कोना होता है जहां तीन रेखाएं जो कि एक घन के किनारे होते हैं वे आकर मिलते हैं। एक घन में आठ किनारे होते हैं।

किनारे (edge) : एक घन में बारह किनारे होते हैं। ये किनारे फलकों की भुजाएं होती हैं। एक घन के बारह के बारह  किनारे समान लम्बाई के होते हैं।

फलक विकर्ण (face diagonal) : फलक विकर्ण वे रेखा खंड होते हैं जो विपरीत शीर्षों को जोड़ते हैं। हर एक फलक के किनारे के दो विकर्ण होते हैं तो कुल 12 विकर्ण होते हैं।

घनाभ क्या होता है ?

घनाभ (cuboid) एक ऐसी त्रिआयामी (3d) आकृति है जिसके 6 आयताकार फलक होते हैं। इसी वजह से ऐसी आकृतियों को बहुफलक भी कहा जाता है।

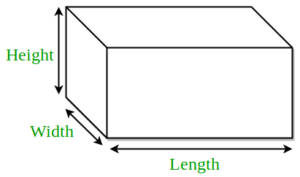
ऊपर दी गयी आकृति में जैसा कि आप देख सकते हैं की इसके सभी फलक आयताकार हैं इस वजह से यह एक घनाभ कहलायेगा। यहाँ इसके तीन परिमाण दे रखे है:

सभी सूत्रों में लम्बाई, चौड़ाई एवं ऊंचाई को इस प्रकार दर्शाया जाता है :

लम्बाई(length) : l

चौड़ाई(breadth/width) : b

ऊंचाई(height) : h

घनाभ के गुणधर्म (properties of cuboid in hindi)

• एक घनाभ के छः फलक होते हैं।
• एक घनाभ के सभी कोण समकोण होते हैं।
• इसके सभी फलक आयताकार होते हैं।
• सभी फलकों का आयताकार होने से तात्पर्य हैं कि हर फलक के जो चार आयाम होते हैं उनमे से एक एक युगल बराबर होना चाहिए। जैसा अगर हम एक ऊपर वाला फलक लेते हैं जिसके आयाम width एवं length होंगे। अब आयताकार होने से मतलब है कि उस फलक की 2 width बराबर एवं 2 length बराबर होनी चाहिए।
• अगर width एवं length बराबर हो जाए तब यह ये एक वर्ग हो जाएगा लेकिन तब भी यह एक घनाभ भी कहलायेगा। क्योंकि यह घनाभ होने की शर्तें पूरी कर रहा है।

सूत्र :

आयतन :

घन का आयतन = a³

घनाभ का आयतन = l*b*h

पूर्ण पृष्ठीय क्षेत्रफल :

घन का पूर्ण पृष्ठीय क्षेत्रफल : 6a²

घनाब का पूर्ण पृष्ठीय क्षेत्रफल = 2 *(lb + bh + hl)

वक्र पृष्ठीय क्षेत्रफल :

घन का वक्र पृष्ठीय क्षेत्रफल : 4a²

घनाभ का वक्र पृष्ठीय क्षेत्रफल = 2*h(l+b)

इस लेख से सम्बंधित यदि आपका कोई भी सवाल या सुझाव है, तो आप उसे नीचे कमेंट में लिख सकते हैं।

गणित से सम्बंधित अन्य लेख:

• बीजगणितीय सर्वसमिकाएँ क्या हैं?
• वर्ग का क्षेत्रफल
• ऊंचाई और दूरी
• भिन्न का जोड़
• भिन्न को घटाना
• नाव और धारा
• शंकु का छिन्नक
• बहुपद के शून्य और गुणनखंड कैसे निकालते हैं?
• पाइथागोरस प्रमेय
• शेषफल प्रमेय