विषय-सूचि
प्रायिकता में इससे पहले हमनें माध्यिका, माध्य एवं बहुलक (mean, median and mode) के बारे में जाना।
सप्रतिबंध प्रायिकता क्या होती है? (conditional probability in hindi)
सप्रतिबंध प्रायिकता ऐसी प्रायिकता होती है जिसमे हम एक घटना के होने के बाद दूसरी घटना के होने की प्रायिकता निकालते हैं।
हम मान लेते हैं कि हमें एक सड़क दुर्घटना होने की प्रायिकता निकालनी है। हमें चालकों की गाडी चलाने की कुशलता के बारे में पता है। इससे हमें इन दो घटनाओं में सम्बन्ध निकालने में मदद मिलेगी। हम जानते हैं की अगर एक चालक गाडी चलाने में प्रवीण है तो उसकी सड़क दुर्घटना होने की कम संभावना होगी।
एक चालाक की गाडी चलाने की प्रवीणता उसकी सड़क दुर्घटना होने पर प्रतिबन्ध लगाती है। यह सप्रतिबंध प्रायिकता का एक उदाहरण है। यह प्रायिकता उन घटनाओं के घटने की संभावना बताती है जिनमें से कुछ घटनाएं पहले ही घाट चुकी हैं।
सप्रतिबंध प्रायिकता को हम p(A|B) से प्रकट करते हैं।
हम इसे साधारण भाषा में ऐसे समझ सकते हैं :
हमारे पास तीन मटके हैं एवं हर मटके में एक लाल एवं एक पीली गेंद है। अब हमें दिया गया है कि पहले मटके में से लाल गेंद निकलने की प्रायिकता ज्ञात कीजिये। यह एक सप्रतिबंध प्रायिकता है। मतलब हमें पहले से जानकारी है की एक घटना हो चुकी है एवं दूसरी घटना पहली घटना पर ही आधारित है।
प्रतिदर्श समष्टि क्या होती है? (sample space in hindi)
प्रायिकता सिद्धांत में प्रतिदर्श समष्टि किसी यादृच्छिक परीक्षण के सभी संभावित परिणामों का समुच्चय होता है, जिसे अमूमन संकेत अथवा द्वारा प्रकट किया जाता है। उदाहरण के अगर हम एक सिक्के को उछालें तो उसकी प्रतिदर्श समष्टि head या tails होगी।
ये भी पढ़ें:
सप्रतिबंध प्रायिकता का सूत्र (conditional probability formula)
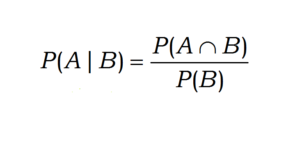
सप्रतिबंध प्रायिकता की प्रमेय (conditional probability theorem)
प्रमेय 1:
अगर A एवं B किसी यादृच्छिक परिक्षण की प्रतिदर्श समष्टि S की घटनाएं हैं तो p(S|B) = p(B|B) = 1 होगा।
प्रमाण : P(S | B) = P(S ∩ B) ⁄ P(B) = P(B) ⁄ P(B) = 1.
प्रमेय 2:
यदि A एवं B प्रतिदर्श समष्टि S की घटनाएं हैं एवं E S की ऐसी घटना है ताकि P(E) ≠ 0, फिर
P((A ∪ B)| E) = P(A | E) + P(B | E) – P((A ∩ B) | E).
प्रमाण: जैसा हम जानते हैं P(A ∪ B) = P(A) + P(B) – P(A ∩ B).
P((A ∪ B) |E) = P((A ∪ B) ∩ E) ⁄ P(E) = P((A ∩ E) ∪ (B ∩ E)) ⁄ P(E).
उदाहरण :
आइये अब हम इस सूत्र से कुछ उदाहरणों को हल करते हैं। हम उन उदाहरणों में यही सूत्र लगाकर हल करेंगे।
उदाहरण 1: एक पासा फेंका गया। अगर 2 का कोई गुणज आने की संभावना A है, एक विषम संख्या संख्या आने की संभावना B है एवं एक सम संख्या आने की संभावना C है।
अगर A घटना B से स्वतंत्र है तो :
P(A |B) = P(A) or, P(A ∩ B) ⁄ P(B) = P(A) or, P(A ∩ B) = P(A). P(B) … (I)
P(B |A) = P(A ∩ B) ⁄ P(A) = P(A).P(B) ⁄ P(A) = P(B)
अतः घटना B भी घटना A से स्वतंत्र है।
इस लेख से सम्बंधित यदि आपके पास कोई भी सवाल या सुझाव है, तो आप उसे नीचे कमेंट में लिख सकते हैं।
गणित के अन्य लेख:
- पाइथागोरस प्रमेय
- शेषफल प्रमेय
- बीजगणितीय सर्वसमिकाएँ क्या हैं?
- वर्ग का क्षेत्रफल
- ऊंचाई और दूरी
- भिन्न का जोड़
- भिन्न को घटाना
- नाव और धारा
- शंकु का छिन्नक
- बहुपद के शून्य और गुणनखंड कैसे निकालते हैं?