विषय-सूचि
त्रिकोणमिति क्या है ?

त्रिकोणमिति गणित की वह शाखा है जिसमें त्रिभुज और त्रिभुजों से बनने वाले बहुभुजों का अध्ययन होता है। त्रिकोण मिति में अगर हम शब्दों का मतलब समझे तो इस शब्द का शाब्दिक अर्थ होता है त्रिभुज का मापन। त्रिकोणमिति में सबसे अधिक महत्वपूर्ण है समकोण त्रिभुज का अध्ययन।
त्रिभुजों और बहुभुजों की भुजाओं की लम्बाई और दो भुजाओं के बीच के कोणों का अध्ययन करने का मुख्य आधार यह है कि समकोण त्रिभुज की किन्ही दो भुजाओं (आधार, लम्ब व कर्ण) का अनुपात उस त्रिभुज के कोणों के मान पर निर्भर करता है।
त्रिकोणमितिय फलन क्या होते हैं ? (trignometric functions)

गणित में त्रिकोणमितीय फलन या ‘वृत्तीय फलन’ कोणों के फलन हैं। ये त्रिभुजों के अध्ययन में तथा आवर्ती संघटनाओं (periodic phenomena) के मॉडलन एवं अन्य अनेकानेक जगह प्रयुक्त होते हैं।
ज्या (sine), कोज्या (कोज) (cosine) तथा स्पर्शज्या (स्पर) (tangent) सबसे महत्व के त्रिकोणमितीय फलन हैं। ईकाई त्रिज्या वाले मानक वृत्त के संदर्भ में ये फलन सामने के चित्र में प्रदर्शित हैं। इन तीनों फलनों के व्युत्क्रम फलनों को क्रमशः व्युज्या (व्युज) (cosecant), व्युकोज्या (व्युक) (secant) तथा व्युस्पर्शज्या (व्युस) (cotangent) कहते हैं।
समकोण त्रिभुज में त्रिकोणमितिय फलन के सूत्र
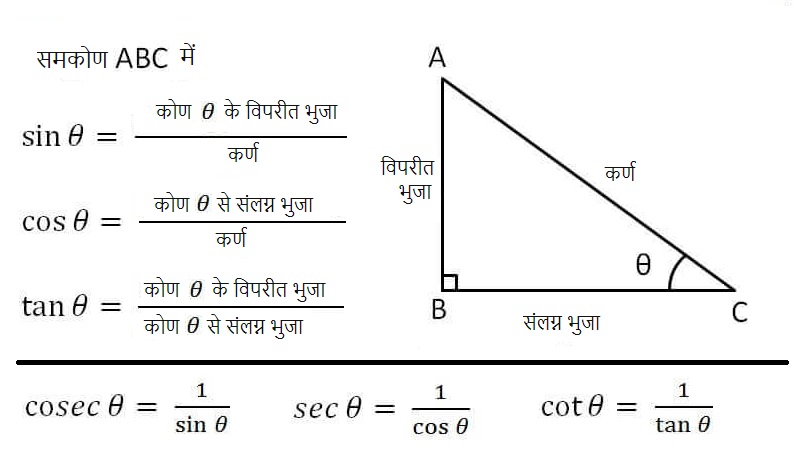
त्रिकोणमिति के मौलिक सूत्र (important formulas of trigonometry)
- sin2α + cos2α = 1
- tan α . cot tan α = 1
- tan α = sin α / cos α = 1 / cot tan α
- cot tan α = cos α / sin α = 1 / tan α
- 1 + tan2a = 1 / cos2a = sec2a
- 1 + cot tan2a = 1 / sin2a = cos sec2a
त्रिकोणमिति सारणी
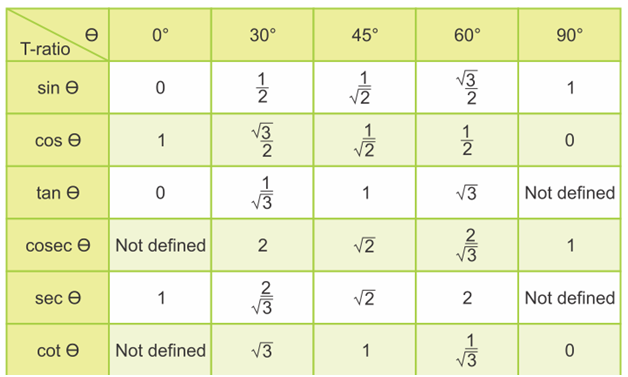
वृत्त खण्डों में त्रिकोणमितिय फलनों का माप
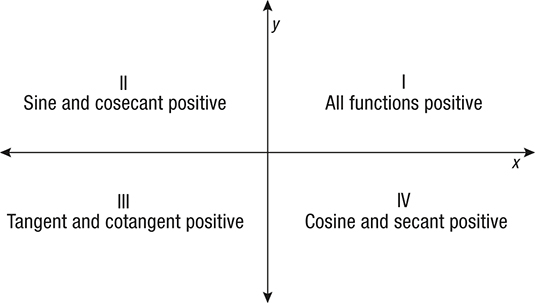
कुछ उदाहरण:
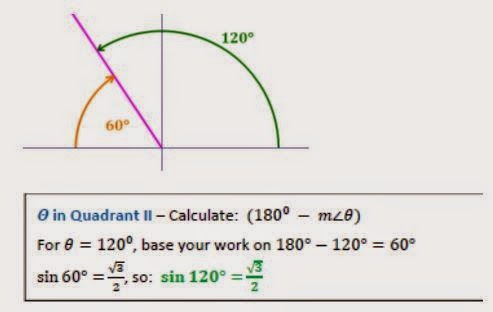
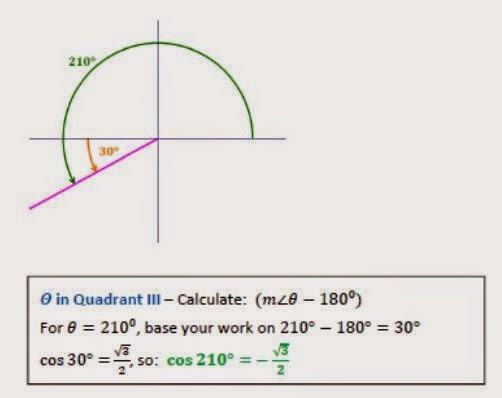
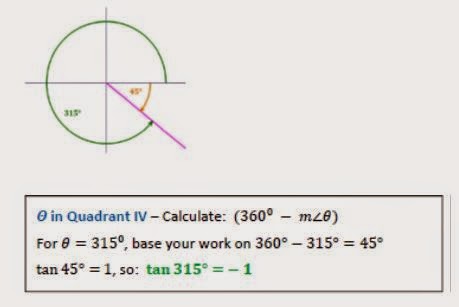
त्रिकोंमिति के कुछ अन्य सूत्र
- cos(X+Y) = cosXcoxY – sinXsinY
- cos(X-Y) = cosXcoxY + sinXsinY
- sin(X+Y) = sinXcoxY + cosXsin
- sin(X-Y) = sinXcoxY – cosXsinY
- tan(X+Y) = [tanX+tanY]/ [1– tanXtanY]
- tan(X-Y) = [tanX-tanY]/ [1+ tanXtanY]
- cot(X+Y) = [cotX+cotY-1]/ [cotX+cotY]
- cot(X-Y) = [cotX+cotY+1]/ [cotX-cotY]
- cosX + cosY = 2cos [(X+Y) / 2] cos[(X-Y)/2]
- sinX + sinY = 2sin [(X+Y) / 2] cos[(X-Y)/2]
- cosX – cosY = – 2sin [(X+Y) / 2] sin[(X-Y)/2]
- sinX + sinY = 2cos [(X+Y) / 2] sin[(X-Y)/2]
- cosXcosY = (1/2) [cos (x-Y) + cos (X+Y)]
- sinXcoxY = (1/2) [sin (x+Y) + sin (X-Y)]
- cosXsinY = (1/2) [sin (x+Y) + sin (X-Y)]
- sinXsinY = (1/2) [cos (x-Y) + cos (X+Y)]
- sin2X – sin2Y = sin (X+Y) sin (X-Y)
- cos2X – cos2Y = – sin (X+Y) sin (X-Y)
- cos2X – sin2Y = cos (X+Y) cos (X-Y)
- sin (2X) = 2 sin X cos X
- cos (2X) = 1 – 2sin2X= 2cos2X – 1
- tan(2X) = 2tanX/[1-tan2X]
- inq= con(900-Φ)
- Cosq= sin(900-Φ)
- tanq= cot(900-Φ)
- cotq= tan(900-Φ)
- secq= cosec(900-Φ)
- cosecq=sec(900-Φ)
कुछ महत्वपूर्ण tricks :




याद रखने योग्य कुछ ज़रूरी बातें :
- tan1. tan2. ……… tan89 = 1
- cot1. cot2 ……. Cot890 = 1
- cos10.cos20…… cos900 = 0
- cos10.cos20…… to (greater than cos900) = 0
- sin10.sin20.sin30 ……… sin1800 = 0
- sin10. sin20 sin30 ….. to (greater than sin1800) = 0
इस लेख से सम्बंधित यदि आपका कोई भी सवाल या सुझाव है, तो आप उसे नीचे कमेंट में लिख सकते हैं।
गणित से सम्बंधित अन्य लेख:
- शंकु का आयतन
- बीजगणितीय सर्वसमिकाएँ क्या हैं?
- वर्ग का क्षेत्रफल
- ऊंचाई और दूरी
- भिन्न का जोड़
- भिन्न को घटाना
- नाव और धारा
- शंकु का छिन्नक
- बहुपद के शून्य और गुणनखंड कैसे निकालते हैं?
- पाइथागोरस प्रमेय
- शेषफल प्रमेय
