हम सभी जानते हैं की एक त्रिभुज के अंदर के तीन कोणों का योग 180 होता है। लेकिन यह हम कैसे जानते हैं?
त्रिभुज के तीनों कोणों का योग सिद्ध करना
हम अब कुछ ज्यामिति की प्रमेयों का प्रयोग करके इस गुण को सिद्ध करेंगे।
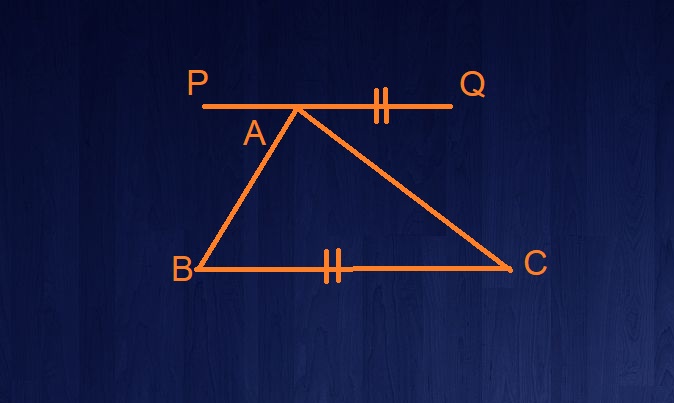
- इस गुणधर्म को सिद्ध करने के लिए सबसे पहले हमें एक त्रिभुज ABC लेना होगा। अब हमें इस त्रिभुज के आधार BC के समांतर एवं त्रिभुज के बाहर एक रेखा खींचनी होगी जो A बिंदु को छूते हुए निकलती है।
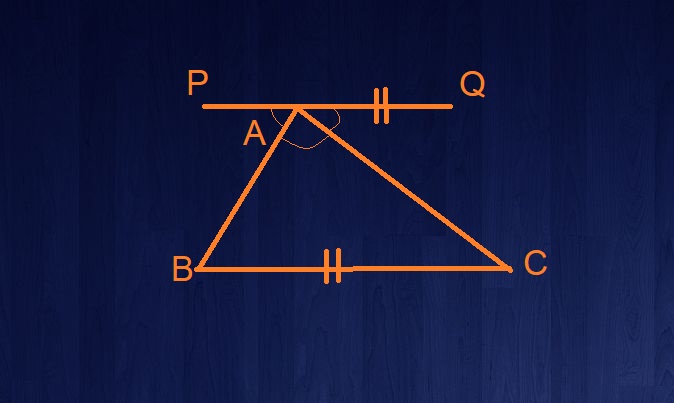
- जैसा कि हम जानते हैं की एक रेखा पर सभी कोणों का योग 180 होता है तो हम निम्न समीकरण बनायेंगे।:
कोण PAB + कोण BAC + कोण CAQ = 180
कोण PAB = कोण ABC [PQ || BC एवं AB तिर्यक रेखा]
कोण QAC = कोण ACB [PQ || BC एवं AC तिर्यक रेखा]
- ऊपर आप जैसा देख सकते हैं A पर बने तीनों कोणों का योग 180 डिग्री होगा एवं कोण PAB एवं ABC, QAC एवं ACB बराबर हो जायेंगे क्योंकि वे Alternate Interior कोण हैं। अब हमारे पास यह समीकरण आ जाता है :
कोण ABC + कोण BAC + कोण ACB = 180 [PAB = ABC, QAC = ACB]
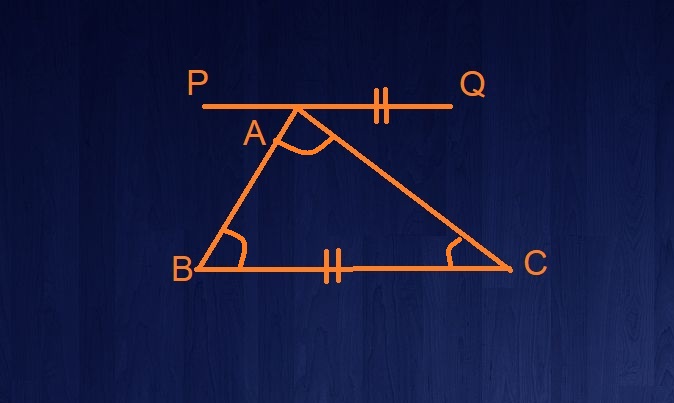
- जैसा कि हम देख सकते हैं ऊपर जो समीकरण है उसमे इस त्रिभुज के अन्दर के तीनों कोण आ गए हैं एवं उनका योग 180 है। अतः इस तरह यह सिद्ध होता है की एक त्रिभुज के अन्दर के तीनों कोणों का योग 180 होता है।
इस लेख से सम्बंधित यदि आपका कोई भी सवाल या सुझाव है, तो आप उसे नीचे कमेंट में लिख सकते हैं।
गणित के अन्य लेख:
- बीजगणितीय सर्वसमिकाएँ क्या हैं?
- वर्ग का क्षेत्रफल
- ऊंचाई और दूरी
- भिन्न का जोड़
- भिन्न को घटाना
- नाव और धारा
- शंकु का छिन्नक
- बहुपद के शून्य और गुणनखंड कैसे निकालते हैं?
- पाइथागोरस प्रमेय
- शेषफल प्रमेय