लघुतम समापवर्त्य कैसे निकालते हैं? परिभाषा

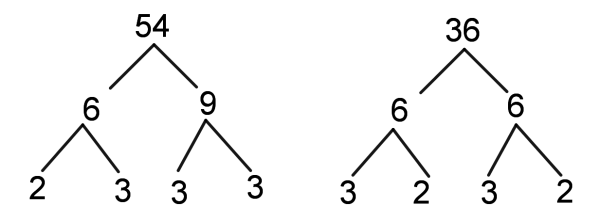
गुणनखंड(Factor) एवं गुणज(Multiple) क्या होते हैं ?

अगर हम कोई दो संख्याएं लेते हैं एवं उन दो संख्याओं में से पहली संख्या दूसरी संख्या को पूरी तरह विभाजित कर रही है तो पहली संख्या दूसरी संख्या की गुणनखंड एवं दूसरी संख्या पहली संख्या की गुणज होगी।

उदाहरण :

4 संख्या 16 संख्या का एक गुणनखंड है एवं 16 संख्या 4 संख्या का एक गुणज है।

लघुतम समापवर्त्य क्या होता है ?

लघुतम समापवर्त्य ( ल. स.)  या Lowest Common Multiple (LCM) वह सबसे छोटी संख्या है जो दी गयी सभी संख्यायों को पूर्णतया विभाजित करती है।

लघुतम समापवर्त्य कैसे निकालते हैं ?

1. संपूर्ण गुणनखंड विधि
2. अभाज्य गुणनखंड विधि
3. विभाजन विधि

1. संपूर्ण गुणनखंड विधि

यह तरीका सबसे ज्यादा कारगर तब रहता है जब आप ऐसी दो संख्याओं का ल.स. निकाल रहे हो जो 10 से कम हों। अगर आप 10 से बड़ी संख्याओं का ल.स. निकाल रहे तो कोई दूसरा तरीका इस्तेमाल करें।

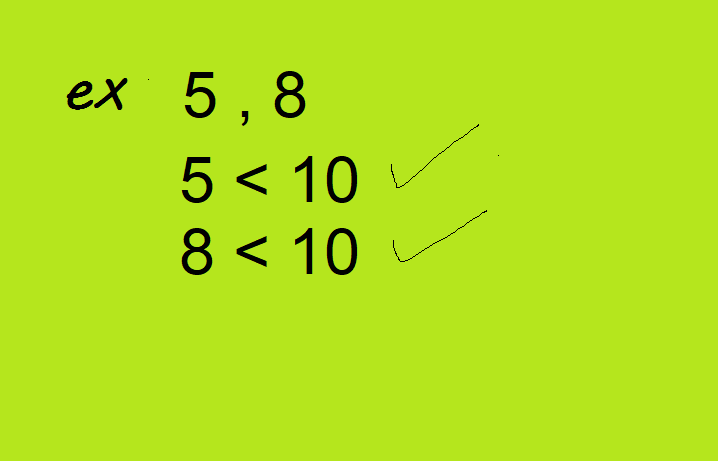
• सबसे पहले जो दो संख्याएं है उनके शुरू के कुछ गुणज की सूचि बनाइये। अगर हम कोई दो संख्याएं लेते हैं एवं उन दो संख्याओं में से पहली संख्या दूसरी संख्या को पूरी तरह विभाजित कर रही है तो पहली संख्या दूसरी संख्या की गुणनखंड एवं दूसरी संख्या पहली संख्या की गुणज होगी।

• दोनों संख्याओं के गुणजों की सूचि बनाने के बाद हमें दोनों संख्याओं के गुणज में जो समान हैं उन्हें ढूँढना है। यही वह संख्या होगी जो ऊपर दी गयी दोनों संख्याओं की लघुतम समापवर्त्य होगी।

• जैसा कि आपने देखा हमारे पास दो संख्याएं थी 5, 8 जिनका लघुतम समापवर्त्य निकला 40 तो आप देख सकते हैं की अगर संख्याएं 10 से छोटी हैं तभी आप इस तरीके से लघुतम समापवर्त्य निकाले नहीं तो इसमें बहुत ज्यादा देर लग जायेगी और ये बहुत लम्बा हो जाएगा।

2. अभाज्य गुणनखंड विधि

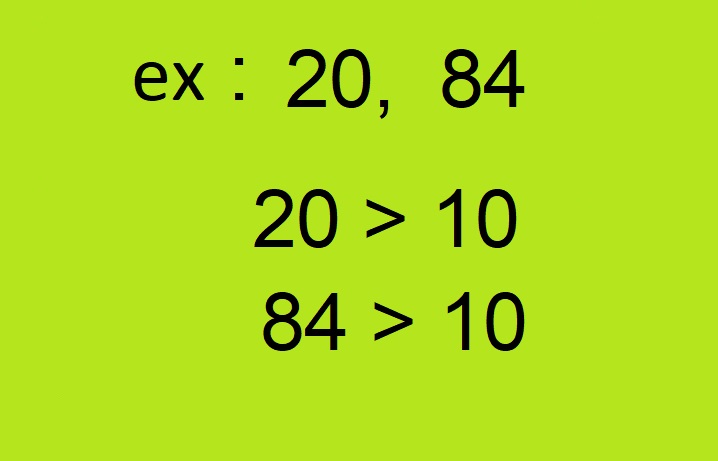
• यह तरीका सबसे ज्यादा कारगर तभी होता है जब वे दोनों संख्याएं जिनका हमें लघुतम समापवर्त्य निकालना है 10 से बड़ी हों। अगर संख्याएं इससे छोटी हैं तो पिछला तरीका इस्तेमाल करें वह 10 से छोटी संख्ययों के लिए है। उदारहण के लिए अगर आपकी संख्याएं 20 एवं 84 हैं तो आप ये तरीका इस्तेमाल कर सकते हैं।

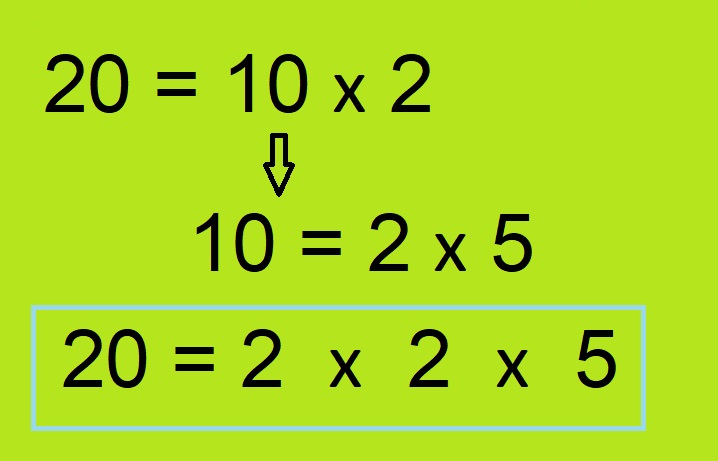
• अब पहली संख्या है उसके गुणनखंडो की सूचि बनाइये। जैसे : 20 = 2 * 2 *5 .

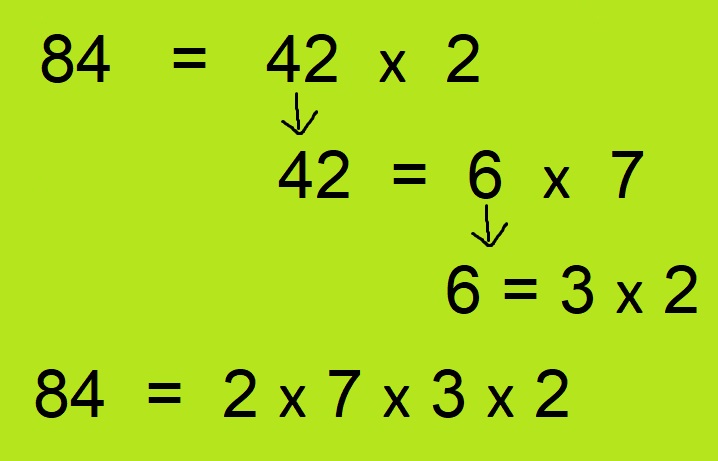
• इसके बाद जैसा आप ऊपर देख सकते हैं की आपको दूसरी संख्या के गुणनखंड की सूचि बनानी है। ये इस संख्या के अभाज्य गुणनखंड होंगे। किसी संख्या का गुणनखंड जो उस गुणनखंड के अतिरिक्त किसी और संख्या से विभाजित न हो वह उस संख्या का अभाज्य गुणनखंड होता है।

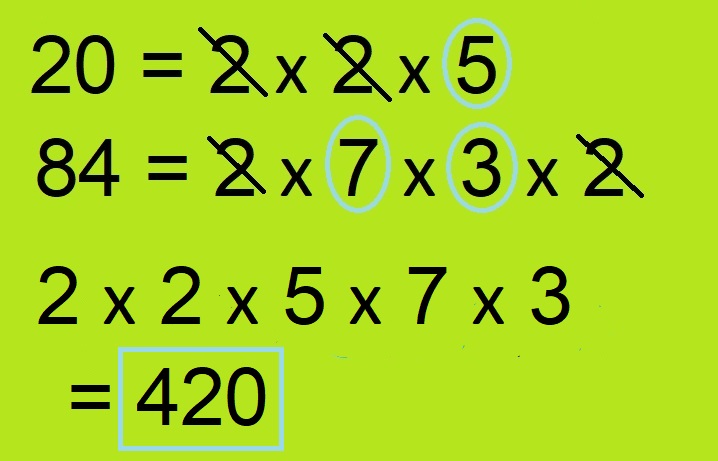
• अब ऐसे गुणनखंड जो दोनों ही संख्यायों में आ रहे हैं उन्हें एक दुसरे से काट दे और एक बार लिखे। जैसे 20 के गुणनखंड में 2 दो बार आ रहा है तो आखिरी में 2 दो बार ही लिखा जाएगा। अब जो गुणनखंड बाख गए उन्हें ऐसे के ऐसे उनसे जोड़ दीजिये। अब ये ऐसा बन जाएगा।: 2*2*5*7*3 अब इन संख्यायों को गुना करने पर जो संख्या आएगी वही संख्या 84, 20 की लघुतम समापवर्त्य होगी।
• इस तरह हम अभाज्य विभाजन तरीके से किन्ही दो संख्या जो 10 से बड़ी होती हैं उनका लघुतम समापवर्त्य निकाल लेते हैं। इस तरीके का प्रयोग करने एक शर्त होती है वो यह होती है की वे दोनों संख्याएं 10 से बड़ी होनी चाहिए। अगर वे संख्याएं 10 से छोटी हैं तो उनका लघुतम समापवर्त्य संपूर्ण गुणनखंड विधि से निकाला जा सकता है।

3. विभाजन विधि

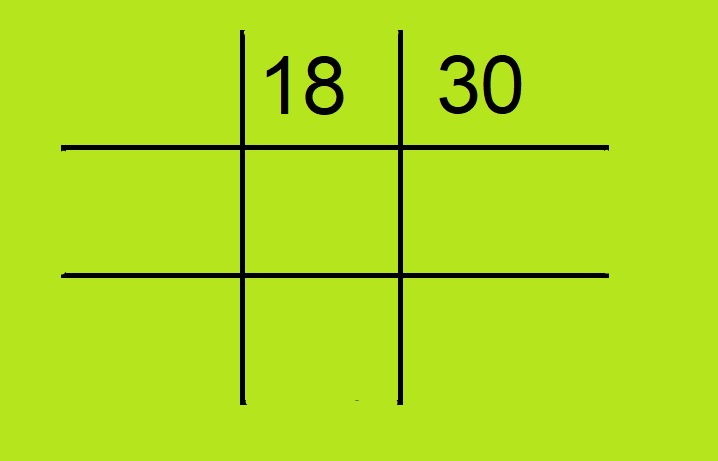
• सबसे पहले हम दी गयी संख्याएं जिनका लघुतम समापवर्त्य निकालना है उन्हें हम ऐसे खानों में लिख लेंगे। पहली संख्या को हम ऊपरी मध्य वर्ग में लिख लेंगे एवं दूसरी संख्या को उसके दायीं और लिख लेंगे।

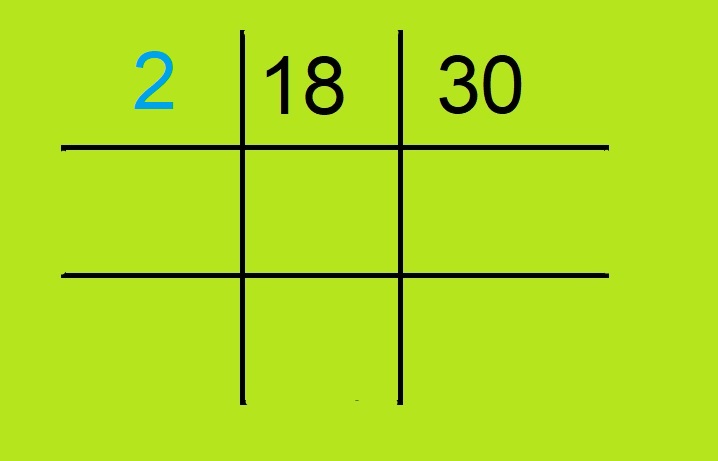
• अब हम उन दोनों का छोटे से छोटा गुणनखंड लिखेंगे जो उन दोनों संख्यायों को विभाजित करदे। उदाहरण के लिए हमारे पास दो संख्याएं है : 18, 30 जिनका सबसे छोटा अभाज्य गुणनखंड 2 है। इसे हम 18 के बाएं वाले वर्ग में लिख देंगे।

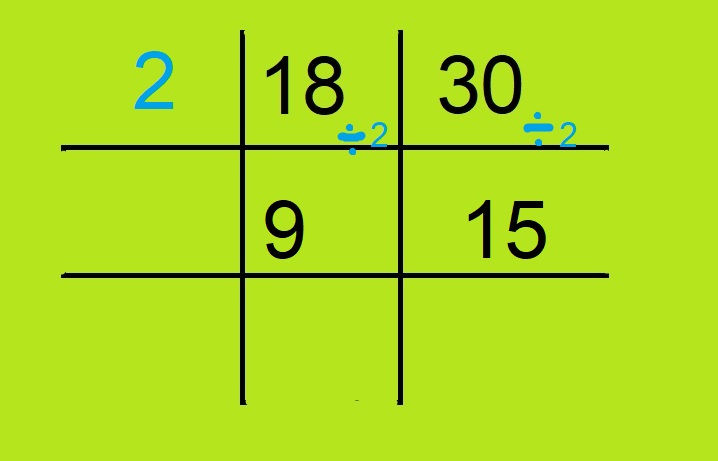
• अब हमने जो 2 लिखा उसका दोनों संख्याओं में भाग देंगे और जो आएगा क्रम से उन्हीं के नीचे लिख देंगे।  जैसे 18 को 2 से भाग देने पर 9 आएगा एवं 30 को 2 से भाग देने से 15 आएगा। हम 9 को 18 के नीचे वाले वर्ग में लिख देंगे एवं 15 को 30 के नीचे वाले वर्ग में लिख देंगे।

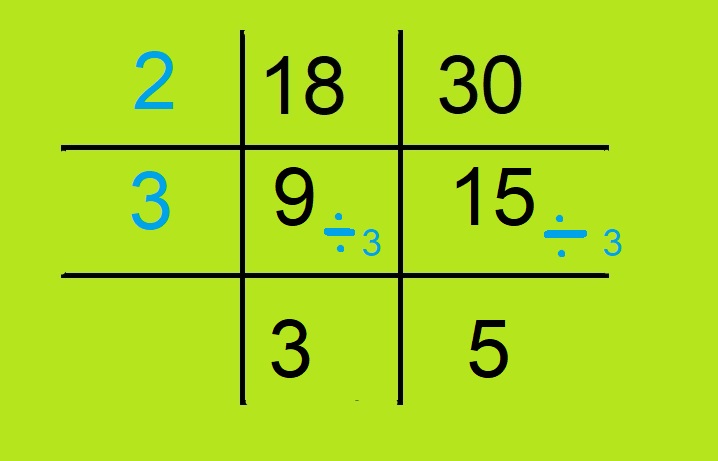
• अब हम एक ऐसी संख्या संख्या खोजेंगे जो संख्या 9 एवं 15 की अभाज्य गुणनखंड होगी। जैसा कि हम देख सकते हैं 9 एवं 15 का अभाज्य गुणनखंड 3 ही होगा। अतः हम 9 एवं 15 के बायीं और 3 लिख देंगे। अब हम 9 एवं 15 में 3 का भाग देकर जो दो संख्या आएँगी उन्हें क्रम से 9 एवं 15 के नीचे लिख देंगे।

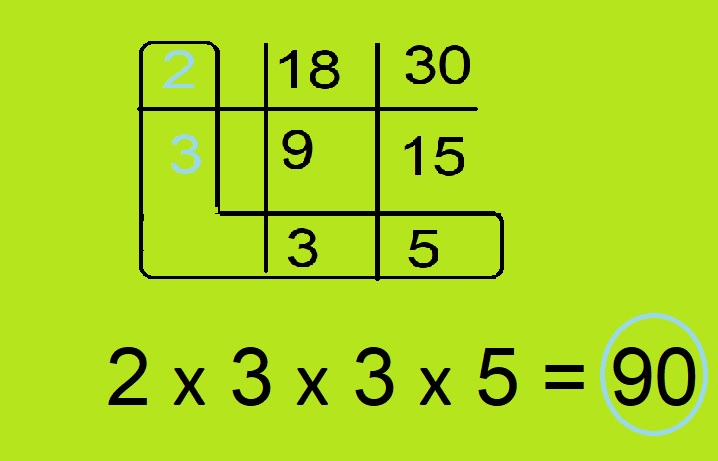
•  अब हमारे पास दो संख्याये हैं जो हैं 3 एवं 5 हैं। इन दोनों का कोई भी एक सामान अभाज्य गुणनखंड नहीं है। अतः अब हम वे जो दो संख्याएं जिनसे हमने पहले दो संख्यायों को भाग दिया उन्हें निचे लिखते हैं वे हैं : 2 * 3 और अब हम इनके साथ जो दो संख्याएं बाख गयी जो आगे विभाजित नहीं हो सकती उन्हें इनके साथ लिखेंगे।
• अब यह ऐसा हो जाएगा : 2 * 3 * 3 * 5
• इन संख्यायों को गुना करने पर हमें 90 मिलेगा। अतः 18 एवं 30 का लघुतम समापवर्त्य 90 होगा। 90 वह सबसे छोटा गुणज है जिसे ये दोनों संख्याएं पूरा विभाजित कर सकती हैं। अतः हमने लघुतम समापवर्त्य ज्ञात कर लिया है।

इस प्रक्रिया से हम दूसरी संख्याओं का भी लघुतम समापवर्त्य ज्ञात कर सकते हैं।

[ratemypost]

आप अपने सवाल एवं सुझाव नीचे कमेंट बॉक्स में व्यक्त कर सकते हैं।