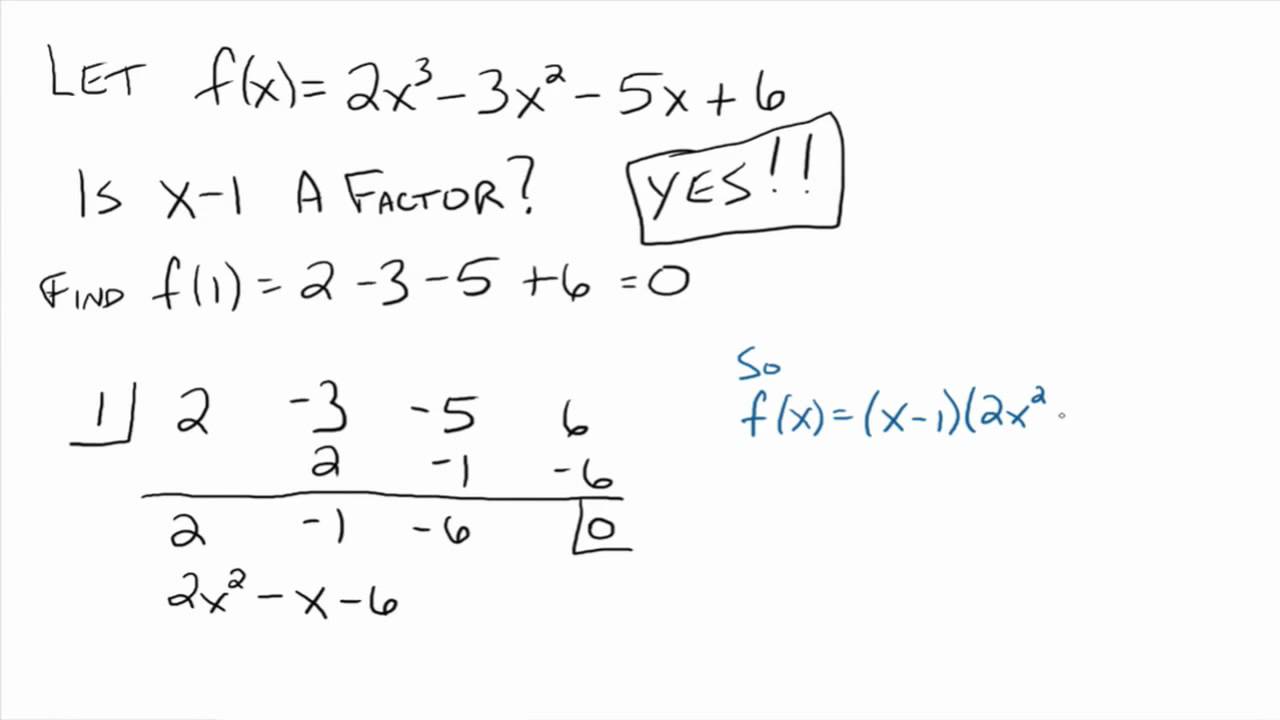विषय-सूचि
शेषफल प्रमेय क्या है? (remainder theorem in hindi)
शेषफल प्रमेय से हम किसी एक बहुपद को बिना भाग किये शेषफल निकाल सकते हैं।
जब हम एक बहुपद का भाग करते हैं तो हम उसे ऐसे लिख सकते हैं :
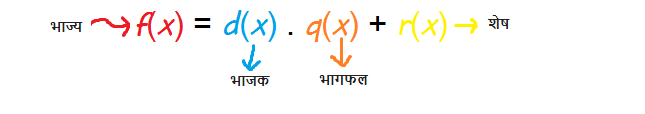
हम 2x2 – 5x – 1 को x – 3 से भाग देते हैं :
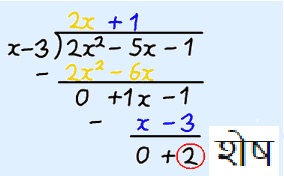
जैसा कि आपने देखा हमें भाग देने पर 2x + 1 उत्तर या भागफल मिला लेकिन इसके साथ ही 2 शेषफल भी मिला।
- q(x) = 2x + 1
- r(x) = 2
हम इसे f(x) = d(x) . q(x) + r(x) के रूप में ऐसे लिख सकते हैं :
2x2 – 5x – 1 = (x-3)(2x + 1) + 2
शेषफल प्रमेय (remainder theorem examples)
जब हम f(x) को एक साधारण बहुपद x – c से भाग देते हैं तो हमें यह प्राप्त होता है :
f(x) = (x – c) . q(x) + r(x)
जैसा हम जानते हैं कि x – c कि डिग्री 1 है तो r(x) की डिग्री 0 होनी चाहिए जिससे ये r एक constant हो जाएगा।
f(x) = (x – c) . q(x) + r
अब हम देखेंगे की r को c के बराबर रखने से क्या होगा :
f(c) = (c – c) . q(c) + r
f(c) = (0) . q(c) + r
f(c) = r
जैसा कि हम देख सकते हैं की जब हम एक बहुपद f(x) को x – c से भाग देते हैं तो शेषफल f(c) आता है।
तो अब हमें पता चल गया है की अगर हमें शेषफल ज्ञात करना है तो हमें असल में भाग करने कि ज़रुरत नहीं है हमें बस f(c) ढूँढना है क्योंकि वह शेषफल के बराबर होता है।
अन्य उदाहरण :
एक बहुपद 2x2 – 5x – 1 को x – 3 से बिना भाग दिए शेषफल ज्ञात करें :
- जैसा कि हमने ऊपर प्रक्रिया में देखा था की शेषफल ज्ञात करने के लिए वास्तविकता में x – 3 से भाग नहीं देना होगा बस हमें f(3) ज्ञात करना होगा और शेषफल उसके बराबर होगा।
f(x) = 2x2 – 5x – 1
- f(3) ज्ञात करने के लिए हमें पूरे बहुपद में x कि जगह 3 रखना होगा एवं हल करना होगा।
f(3) = 2(3)2 – 5(3) – 1
= 2*9 – 5*3 – 1
= 18 -15 -1
= 2
- अतः इसका शेषफल हमने बिना भाग दिए ही निकाल लिया है जो कि 2 है .तो जैसा कि आप समझ गए होंगे सहेश्फल निकालने के लिए हमें असल में भाग नहीं देना पड़ता इसे बिना भाग दिए भी ज्ञात किया जा सकता है।
एक बहुपद 2x2 – 5x – 1 को x – 5 से बिना भाग दिए शेषफल ज्ञात करें :
- जैसा कि आप देख सकते हैं हमें एक बहुपद दिया गया है एवं हमें बिना भाग दिए उसका शेषफल निकालना है। जैसा कि हमने ऊपर प्रक्रिया में देखा था कि हम शेषफल बिना भाग करे भी निकाल सकते हैं। उसके लिए हमें बस f(c) निकालना पड़ेगा। तो चलिए हम इस बहुपद का f(c) निकालते हैं।
f(x) = 2x2 – 5x – 1 , c = 5
- जैसा कि हम ऊपर देख सकते हैं की c 5 के बराबर है। तो अब हमें c निकालने के लिए बहुपद में सभी x कि जगह पर 5 लगाना होगा इससे f(c) आ जाएगा।
f(5) = 2(5)2 – 5(5) – 1 = 2*25 – 5*5 -1
= 50 – 25 -1
= 24
- तो जैसा कि हमने देखा की x कि जगह c रखने से हमारे पास 24 आ गया जोकि f(c) है। जैसा कि हम जानते हैं कि f(c) शेषफल के बराबर होता है। अतः शेषफल 24 होगा। एक और बार हमने बिना भाग दिए शेषफल निकाल दिया है।
इस लेख से सम्बंधित यदि आपका कोई भी सवाल या सुझाव है, तो आप उसे नीचे कमेंट में लिख सकते हैं।