शंकु : परिभाषा, गुणधर्म, क्षेत्रफल एवं आयतन

शंकु की परिभाषा (definition of cone in hindi)

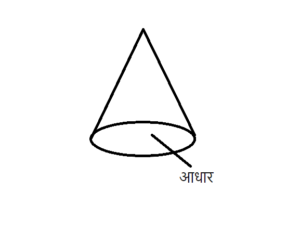
शंकु(cone) एक ऐसी त्रिआयामी(3d) आकृति है जिसका एक गोलाकार आधार होता है एवं जिसका शीर्ष एक बिंदु होता है। हम अगर एक समतल में देखें तो शंकु ऐसे रेखा खण्डों से बना होता है जो शीर्ष पर बिंदु है उसे आधार के सभी बिंदु से जोड़ते हैं। ऐसा होने पर शंकु बनता है।

इससे पहले हमनें शंकु का छिन्नक के बारे में पढ़ा।

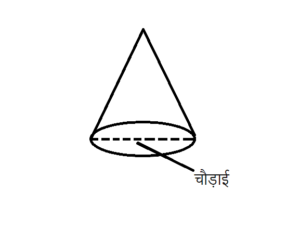
ऊपर दी गयी आकृति में जैसा कि आप देख सकते हैं यहाँ एक गोला कार आधार है एवं सबसे ऊपर शीर्ष पर एक निश्चित बिंदु है। अतः यह त्रिआयामी आकृति एक शंकु कहलाएगी।

शंकु के गुणधर्म (properties of a cone in hindi)

आइये अब हम इस आकृति के कुछ गुणधर्मों के बारे में चर्चा करते हैं :

• फलक : एक शंकु में केवल एक फलक होता है एवं वह फलक गोलाकार होता है। यह शंकु का नीचे का हिस्सा होता है। इसे शंकु का आधार भी कहा जाता है।

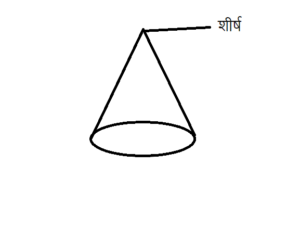
• शीर्ष : एक शंकु में एक शीर्ष होता है। शंकु के किनारों को घुमाया जाता है एवं उन्हें एक बिंदु पर मोड़ दिया जाता है जिससे हमें शंकु का शीर्ष मिलता है।

• एक शंकु की चौड़ाई उसके गोलाकार फलक का व्यास होता है।

शंकु का क्षेत्रफल (area of a cone in hindi)

शंकु का पूर्ण पृष्ठीय क्षेत्रफल (total surface area of cone)

शंकु के पूर्ण पृष्ठीय क्षेत्रफल का सूत्र निम्न होता है :

 पूर्ण पृष्ठीय क्षेत्रफल = πr (l+r) 

यहाँ r आधार की त्रिज्या है एवं l शंकु की तिर्यक ऊंचाई है।

यह हम इस तरह से निकाल सकते हैं :

वक्र पृष्ठ का क्षेत्रफल =  πrl 

आधार का क्षेत्रफल = πr²

जब हम इन दोनों को जोड़ते हैं :

 = πrl  + πr² 

=  πr (l+r) 

शंकु का वक्र पृष्ठीय क्षेत्रफल :

शंकु के वक्र पृष्ठीय क्षेत्रफल का सूत्र निम्न होता है :

वक्र पृष्ठीय क्षेत्रफल = πrl 

यहाँ r आधार की त्रिज्या है एवं l शंकु की तिर्यक ऊंचाई है।

शंकु की तिर्यक ऊंचाई:

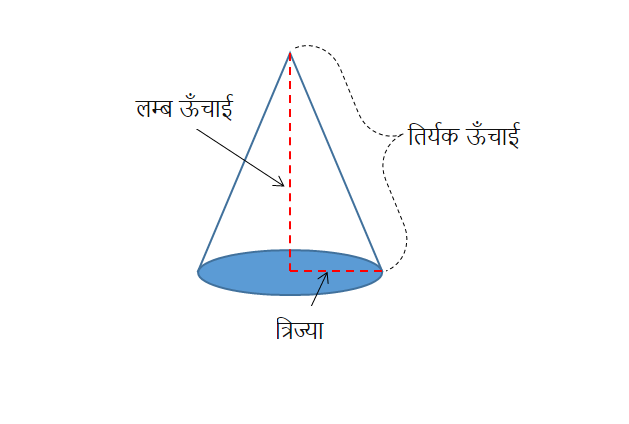
एक शंकु की तिर्यक ऊंचाई को l से चिन्हित या सूचित किया जाता है। अगर हमें यह नहीं दे रखी है तो हम इसे इस प्रकार निकाल सकते है :

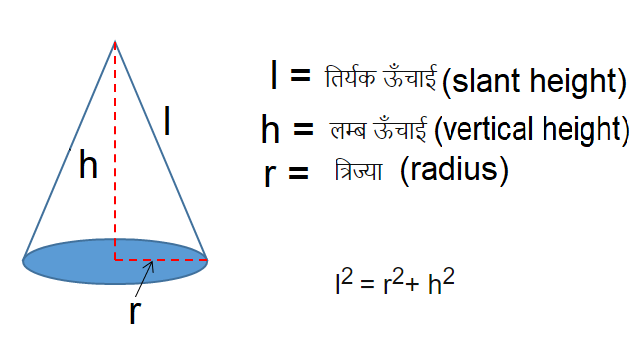
l² = r²+ h² 

जहाँ r गोलाकार आधार की त्रिज्या होती है एवं h शंकु की ऊंचाई होती है। यह हम पाइथागोरस प्रमेय से करते हैं क्योंकि एक शंकु के अन्दर एक समकोण त्रिभुज बनता है।

शंकु का आयतन (volume of a cone in hindi)

जैसा कि हम जानते हैं शंकु एक त्रिआयामी आकृति है जिसका गोलाकार आधार होता है। इसकी बनावट के आधार पर हम शंकु का आयतन समान आधार वाले बेलन के आयतन का तीसरा हिस्सा मानते हैं।

बेलन का आयतन = πr²h 

शंकु का आयतन = ¹/₃ बेलन का आयतन 

अतः

शंकु का आयतन = ¹/₃ πr²h

ऊपर दिए गए विभिन्न सूत्रों से हम एक शंकु का पूर्ण पृष्ठीय क्षेत्रफल, वक्र पृष्ठीय क्षेत्रफल एवं आयतन निकाल सकते है।

उदाहरण:

आइये अब हम उदाहरणों के साथ शंकु का क्षेत्रफल निकालना सीखेंगे :

उदाहरण 1: एक शंकु जिसके गोलाकार आधार की त्रिज्या 10 cm  एवं तिर्यक ऊंचाई 30 cm  है। इस शंकु का पृष्ठीय क्षेत्रफल ज्ञात कीजिये। (ध्यान दीजिये अगर सवाल में सिर्फ पृष्ठीय क्षेत्रफल निकालने के लिए कहा गया है तो हमें पूर्ण पृष्ठीय क्षेत्रफल निकालना होगा)

हल : हमें सबसे पहले यह देखना है कि इस शंकु की त्रिज्या एवं तिर्यक ऊंचाई कितनी है एवं फिर इसे हमें एक सूत्र में रखना है।

त्रिज्या : 10 cm 

ऊंचाई : 30 cm

अब हमें इन दोनों का माप पता चल गया है तो इसे हम अब सूत्र में रखेंगे।

शंकु का पूर्ण पृष्ठीय क्षेत्रफल =  πr (l+r) 

अब हमें इस सूत्र में वैल्यूज रखनी हैं :

= ²²/₇ * 10 (30 + 10)

= 1257.14 cm²

इस प्रकार हम एक शंकु का क्षेत्रफल निकालते हैं।

गणित के अन्य लेख:

• पाइथागोरस प्रमेय
• शेषफल प्रमेय
• बीजगणितीय सर्वसमिकाएँ क्या हैं?
• वर्ग का क्षेत्रफल
• ऊंचाई और दूरी
• भिन्न का जोड़
• भिन्न को घटाना
• नाव और धारा
• बहुपद के शून्य और गुणनखंड कैसे निकालते हैं?
• रैखिक समीकरण