विषय-सूचि
मध्य बिंदु प्रमेय की परिभाषा (midpoint theorem in hindi)
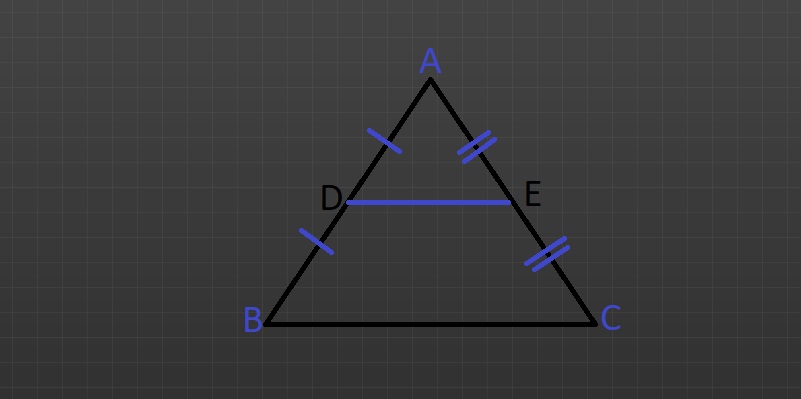
मध्य बिंदु प्रमेय के अनुसार अगर हम एक त्रिभुज की दो भुजाओं के मध्य बिन्दुओं को जोड़ने वाली एक रेखा खींचते हैं तो वह रेखा उस त्रिभुज की तीसरी भुजा के समान्तर होगी। ऊपर दिए गए त्रिभुज में जैसा कि हम देख सकते हैं हमने त्रिभुज ABC में AB एवं AC के मध्य बिन्दुओं को जोड़ने वाली DE रेखा खींची। मध्य बिंदु प्रमेय के अनुसार यह रेखा BC के समान्तर होगी।
मध्य बिंदु प्रमेय की पुष्टि (midpoint theorem explanation in hindi)
- इस प्रमेय की पुष्टि करने के लिए हमें सबसे पहले एक त्रिभुज बनाना होगा।
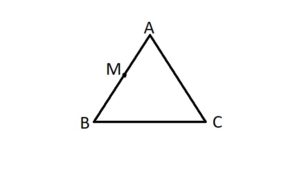
- जैसा कि आप ऊपर दी गयी छवि में देख सकते हैं हमने एक त्रिभुज बनाया जिसका नाम हैं ABC है। हमने इसकी भुजा AB का मध्य बिंदु M नामांकित किया।
- अब हम भुजा AB एवं AC के मध्य बिन्दुओं को जोड़ने वाली एक रेखा खीचेंगे।
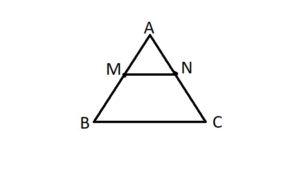
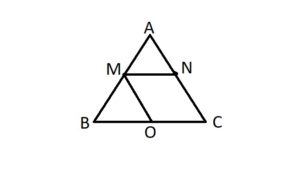
- जैसा कि आप ऊपर छवि में देख सकते हैं हुकने भुजा AB एवं AC के मध्य बिन्दुओं को जोड़ने वाली एक रेखा बनायी है एवं उसको MN नाम दिया। अब हमें पुष्टि करनी है की MN भुजा BC के समान्तर है।
- अब हमें M से निकलती हुई एक ऐसी रेखा खींचनी है जो BC भुजा के मध्य बिंदु को जोडती है एवं AC के समान्तर है।

- जैसा कि हम उपर छवि में देख सकते हैं हमने AC के समांतर एवं BC के मध्यबिंदु को जोड़ने वाली रेखा MO खींची।
- अब हमें त्रिभुज AMN को त्रिभुज BMO से सर्वांग्स्म सिद्ध करना है। हम इन दोनों त्रिभुज को सर्वांग्स्म इस तरह सिद्ध करेंगे :
AM = BM [मध्यबिंदु]
कोण AMN = कोण ABC
कोण BOM = कोण BCN = कोण MNA
कोण BMO = कोण MAN
इस प्रकार BMO एवं MAN त्रिभुज सर्वांग्स्म हुए [ASA]
- अतः AN = MO = NC एवं MN = BO = OC
- चूंकि मध्य बिन्दु विरले हैं, और बिन्दुओं को जोड़ने वाली रेखाएं विरली हैं, यह कथन सिद्ध होता है।
ऊपर दी गयी विडियो में भी मध्य बिंदु प्रमेय यानी मिड पॉइंट थ्योरम को आसान भाषा में समझाया गया है।
इस लेख से सम्बंधित यदि आपका कोई भी सवाल या सुझाव है, तो आप उसे नीचे कमेंट में लिख सकते हैं।
गणित के अन्य लेख:
- बहुपद के शून्य और गुणनखंड कैसे निकालते हैं?
- भिन्नों को घटाना
- शेषफल प्रमेय
- बीजगणितीय सर्वसमिकाएँ क्या हैं?
- भिन्न का जोड़
- वर्ग का क्षेत्रफल