विषय-सूचि
त्रिभुज की परिभाषा (definition of triangle in hindi)
त्रिभुज तीन रेखाओं से बनी हुई एक बंद आकृति होती है।
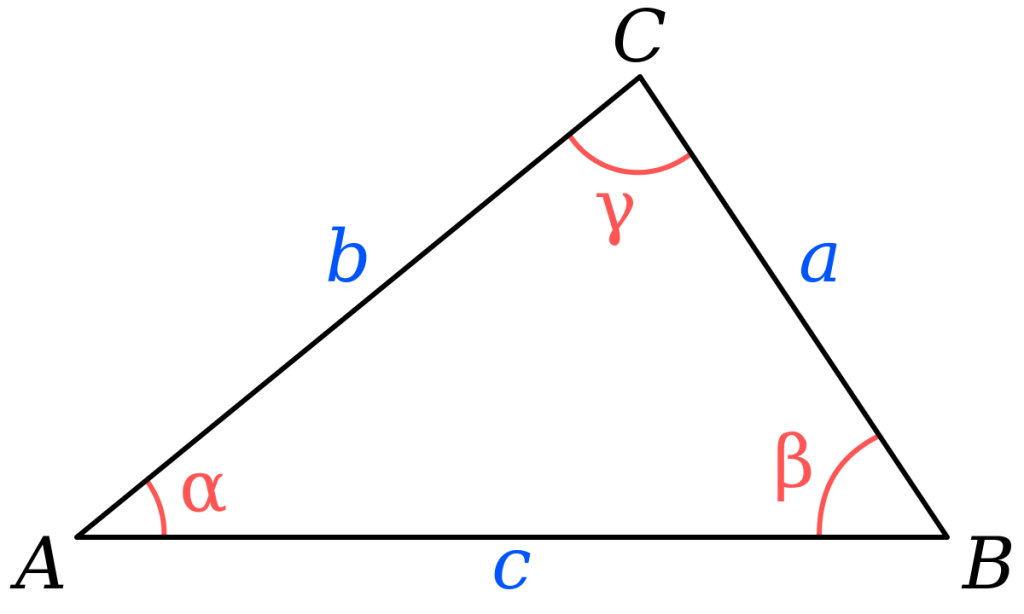
भुजा (side): जिन तीन रेखा खण्डों से त्रिभुज बनता है वे रेखा खंड त्रिभुज की भुजाएं कहलाती हैं। ऊपर दिए गए त्रिभुज में AB, BC व CA त्रिभुज ABC की भुजाएं कहलाएंगी।
शीर्ष : त्रिभुज कि भुजाओं पर जो प्रतिच्छेद बिंदु(दो भुजाओं के मिलन बिंदु) होता है वह शीर्ष कहलाता है। यहाँ दो भुजाएं आकर मिलती हैं। एक त्रिभुज में तीन शीर्ष होते हैं। ऊपर दिए गए त्रिभुज में तीन जगहों पर प्रतिछेद बिंदु है। A बिंदु पर भुजा AB व AC आकर मिल रही है, B बिंदु पर भुजा AB ओर CB आकर मिल रही हैं और C बिंदु पर AC और CB भुजाएं आकर मिल रही हैं। अतः इस त्रिभुज में A, B व C तीन शीर्ष हैं।
त्रिभुज के कोण : शीर्ष पर बनने वाले कोणों को त्रिभुज के कोण कहते हैं। चूंकि त्रिभुज में तीन शीर्ष होते है इसलिए एक त्रिभुज में तीन ही कोण होंगे। त्रिभुज के तीन कोण निम्न हैं: ∠ABC, ∠BCA, ∠BAC
अभिलम्ब (normal) : एक त्रिभुज में किसी एक शीर्ष से विपरीत भुजा पर डाला गया लम्ब अभिलम्ब कहलाता है।
त्रिभुज एक साधारण आकृति है जिसकी भुजाओं, आंतरिक कोणों व बाहरी कोणों पर आधारित कई विशेषताएं होती हैं।
त्रिभुज के प्रकार (types of triangles in hindi):
भुजाओं के आधार पर त्रिभुज के प्रकार (types of triangle on basis of sides)
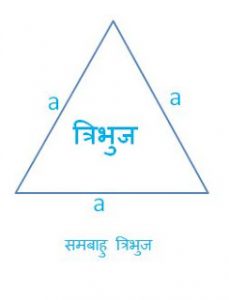
- समबाहु त्रिभुज (equilateral triangle): जब एक त्रिभुज कि तीनो भुजाएं सामान होती हैं एवं प्रत्येक कोण 60 अंश का होता है।
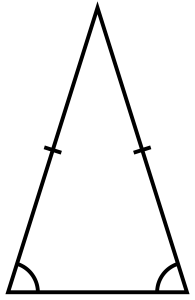
2. समद्विबाहु त्रिभुज (isosceles triangle) : जब किसी त्रिभुज कि कोई दो भुजायें समान होती हैं। सामान भुजाओं के विपरीत बनने वाले कोण भी समान होते हैं। नीचे दी गयी आकृति एक समद्विबाहु त्रिभुज है।
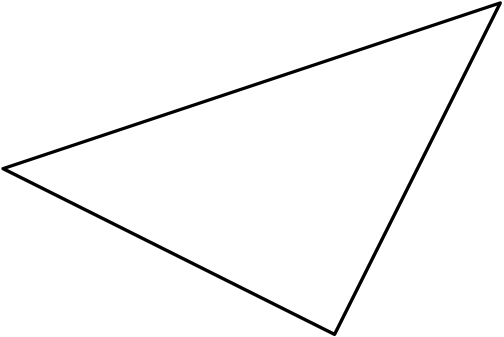
3. विषमबाहु त्रिभुज (scalene triangle): इस त्रिभुज की सारी भुजाएं आपस में असमान होती हैं। सारी भुजाओं के असमान हों से सभी कोण भी असमान होते हैं।
कोणों के आधार पर त्रिभुज के प्रकार (types of triangles on basis of angles):
- न्यूनकोण त्रिभुज (acute triangle): ऐसा त्रिभुज जिसके सभी कोण न्यून कोण होता हैं अथवा जिसके सभी कोणों का माप 90 अंश से कम होता है वह त्रिभुज न्यूनकोण त्रिभुज कहलाता है।
2. समकोण त्रिभुज (right angle): ऐसा त्रिभुज जिसका एक कोण 90 अंश का होता है या समकोण होता है उसे हम समकोण त्रिभुज कहते हैं। समकोण त्रिभुज को हम आयताकार त्रिभुज भी कह सकते हैं।
इस त्रिभुज में समकोण के सामने वाली भुजा को कर्ण(hypotenuse) कहते हैं। कर्ण त्रिभुज की सबसे लम्बी भुजा होती है।
पाइथागोरस प्रमेय (Pythagoras theorem): यह समकोण त्रिभुज की तीनों भुजाओं के बीच सम्बन्ध बतानी वाला एक प्रमेय है। इस प्रमेय को आमतौर पर एक समीकरण के रूप में निम्नलिखित तरीके से अभिव्यक्त किया जाता है।
- जहाँ c समकोण त्रिभुज के कर्ण की लंबाई है तथा a और b अन्य दो भुजाओं की लम्बाई है।
त्रिकोण के कुछ मूल धर्म (properties of triangle in hindi)
- त्रिभुज के तीनों कोणों का योग 180 अंश होता है।
- त्रिभुज कि किन्ही भी दो भुजाओं की लम्बाई का योग तीसरी भुजा की लम्बाई से अधिक होता है।
- त्रिभुज के सबसे छोटे कोण के विपरीत भुजा सबसे छोटी भुजा होती है एवं त्रिभुज के सबसे बड़े कोण की विपरीत भुजा त्रिभुज कि सबसे बड़ी भुजा होती है।
- जैसा कि आप ऊपर दिए गए त्रिभुज ABC में देख सकते हैं कि कोण B सबसे बड़ा कोण है एवं इसके विपरीत भुजा AC सबसे लम्बी भुजा है। इसी प्रकार कोण C सबसे छोटा कोण है तो इस कोण के विपरीत भुजा AB सबसे छोटी भुजा है।
- एक त्रिभुज के बाहरी कोण उसके विपरीत आंतरिक कोणों के योग के बराबर होता है। त्रिभुज का यह गुण बाहरी कोण गुण कहलाता है।
- दिए गए त्रिभुज ABC में आप देख सकते हैं कि कोण ACD बाहरी कोण है। बाहरी कोण विशेषता के अनुसार कोण ACD = कोण CAB + कोण ABC होते हैं।
त्रिभुजों में समरूपता एवं सर्वांगसमता (congruency and similarity in triangles in hindi)
जब कुछ आकृतियों एक जैसी दिखाई देती हैं तब वे सर्वांगसम होती हैं। जब दो आकृतियाँ सर्वांगसम होती हैं तो उन्हें हिलाने या घुमाने पर भी वो सर्वांगसम होती हैं।
दो त्रिभुज समरूप होते हैं यदि एक त्रिभुज के प्रत्येक कोण का मान, दूसरे त्रिभुज के (तत्स्थानिक) कोणों के मान के बराबर होता है। समरूप त्रिभुजों में तत्स्थानिक भुजाओं की लंबाइयाँ समान अनुपात में होती हैं, और यह गुण त्रिभुजों में समरूपता स्थापित करने के लिए पर्याप्त है।
त्रिभुज के सन्दर्भ में यदि आपका कोई भी सवाल या सुझाव है, तो आप उसे नीचे कमेंट में लिख सकते हैं।







त्रिभुज के तीनो कोणों का योग 2 समकोण के बराबर होता है?
Triangle ki side se uske angle kA pta kaise chalega ki triangle kaisa h smkon ya adhikkon or nyunkon
Aap geometry ke all theorems pdf me daliye
जब हम यह कहते हैं कि त्रिभुज या किसी भी बहुभुज के बाह्य कोणों का योग 360° होता है । तो इसका मतलब है कि हम संपूरक कोण तथा पूर्ण कोण की परिभाषा को को नकार रहे हैं। यदि इन दोनों परिभाषाओं को मानते हैं तो, त्रिभुज के बाह्य कोणों का जोड़ 900° होगा, 360° नहीं और हम जो योग 360°बता रहे हैं उसे क्रमागत बढ़े बाह्य सम्पूरक कोणों का योग कहना चाहिए ।