विषय-सूचि
घातांक क्या होता है? (exponent in hindi)
घातांक वह संख्या होती है जो हमें बताती है की किसी संख्या को कितने बार खुद से ही गुना करना है। जैसे : 23 में हम देख सकते हैं कि हमें 2 को तीन बार खुद से गुना करना पड़ेगा।
हम 2 को तीन बार खुद से गुना करेंगे तो हमारे पास उसका घन आ जाएगा। तो इसी प्रकार घातांक हमें बताते हैं कि हमें संख्या को कितनी बार खुद से ही गुना करना पडेगा।
घातांक के नियम: (rules of exponent in hindi)
घातांक के मुख्यतः 6 नियम होते हैं वे निम्न है :
नियम 1: a0 = 1
शून्य के अलावा अगर कोई भी संख्या के ऊपर अगर 0 घात है तो उसका मान 1 हो जाएगा।
उदाहरण :
- 80 = 1
जैसा कि आप देख सकते हैं 2 एक संख्या है एवं इसके घात के रूप में 0 या शून्य है। जब ऐसा होता है तो संख्या का मान स्वत ही 1 हो जाता है। यहाँ पर भी 2 कि घात 0 होने से इस संख्या का मान 1 हो गया है।
नियम 2: a-m = 1/am
अगर किसी संख्या की घात में ऋणात्मक चिन्ह है तो फिर वह संख्या 1 के भाग में चली जायेगी एवं उसकी घात धनात्मक हो जायेगी।
उदाहरण :
- 3-3= 1/33 = 1/27
ऊपर दिए गए उदाहरण में जैसा कि आपने देखा की 3 संख्या की घात 3 है लेकिन वह ऋणात्मक है। हम यह भी जानते हैं कि जब ऋणात्मक घात होती है तो वह संख्या 1 के भाग में चली जाती है लेकिन उसकी घात धनात्मक हो जाती है।
नियम 3: am * an = am+n
अगर किन्हीं ऐसी दो संख्याएं जिनका मूल समान है लेकिन घात अलग है उन्हें गुना किया जाता है अगर उन दो संख्याओं को गुना किया जाता है तो उनकी घात का योग हो जाता है।
उदाहरण:
- 22 * 23 = 22+3 = 25
- = 2*2*2*2*2 = 32
जैसा कि आपने देखा ऊपर हमारे पास एक जगह 2 कि घात 2 थी एवं एक जगह 2 कि घात 3 थी। जब हमने उन दोनों संख्याओं को गुना किया तो फिर उन दोनों संख्याओं कि घात का योग हो गया।
नियम 4 : am/an = am-n
अगर किन्हीं ऐसी दो संख्याओं का भाग दिया जाता हैं जिनका मूल ह्या आधार समान है तो उन दोनों संख्याओं की घात घटा हो जाती हैं एवं हम एक ही आधार लेते हैं।
उदाहरण:
- 25/23 = 25-3 = 22 = 4
जैसा कि आपने देखा की ऊपर हमारे पास दो संख्याएं थी जिनका आधार समान the लेकिन उनके घात अलग अलग थे। ऐसी संख्याओं को जब भाग दिया गया तो उनका आधार एक हो गया एवं जो संख्या अंश में थी उसकी घात में से हर वाली संख्या की घात घटा हो गयी।
नियम 5 : (am)n : am*n
अगर कोई संख्या घात के साथ कोष्ठक में होती है एवं कोष्ठक के बाहर भी कोई घात होती है तो दोनों घाटों का गुना होता है। गुना होने बाद जो घात आती है वाही घात उस संख्या कि घात होती है। फिर हम उस संख्या को उतनी बार गुना करके उसका हल निकालते हैं।
उदारहण :
- (22)3 = 26 = 64
ऊपर दिए गए उदाहरण में जैसा कि आपने देखा की हमारे पास संख्या 2 थी जिसकी घात 2 थी एवं कोष्ठक के बहार 3 घात थी तो 2 एवं तीन घात का गुना हो गया। इससे घात 6 हो गयी इससे 2 को 6 बार गुना किया गया जिससे हमारे पास 64 आया।
नियम 6 : am/n =n√am = (n√a)m
उदाहरण :
- 642/3 = (3√64)3 = (4)2 = 16
गणित से सम्बंधित अन्य लेख:
- शंकु का आयतन
- बीजगणितीय सर्वसमिकाएँ क्या हैं?
- वर्ग का क्षेत्रफल
- ऊंचाई और दूरी
- नाव और धारा
- शंकु का छिन्नक
- बहुपद के शून्य और गुणनखंड कैसे निकालते हैं?
- पाइथागोरस प्रमेय
- शेषफल प्रमेय

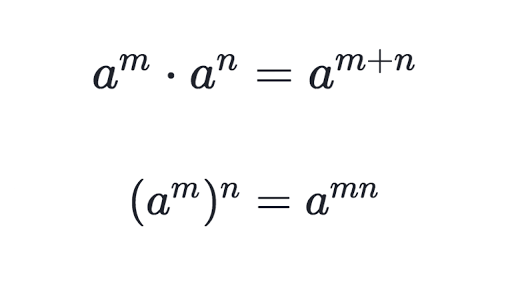
65sqaure-55sqaure
3/7की घात 1789 को किस प्रकार हल करेंगे ।
घातांक के नियम को आपने बहुत अच्छे से समझाया है। लेकिन अगर आपने उदाहरण थोड़ा और दिया होता तो हमे और अधिक मदद मिलती। फिर भी आपको धन्यवाद ।
Good work, Helpful for teacher & students