विषय-सूचि
ऊंचाई और दूरी क्या होती है? (height and distance in hindi)

कक्षा 10 में ऊंचाई एवं दूरी एक महत्वपूर्ण पाठ है। ऊंचाई किसी भी वस्तु का लम्बरूप दिशा में माप होता है। जैसे हमारी ऊंचाई होती है 5 फुट 6 फुट आदि इसी प्रकार चीज़ों की ऊपर से नीचे तक का माप को ही ऊंचाई कहते है।
दूरी किसी भी वस्तु की किसी भी एक बिंदु से दूरी होती है। जैसे कोई चीज़ किसी निश्चित बिंदु से 100 मीटर दूर है या 1 km दूर है इसे दूरी कहते हैं।
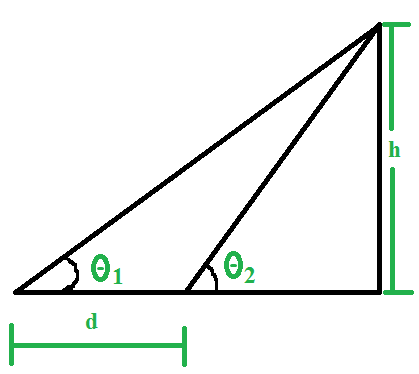
अगर हम एक वस्तु के शीर्ष बिंदु एवं ज़मीन पर एक बिंदु को जोड़ने वाली एक रेखा के बारे में सोचें तो यह रेखा, वास्तु की ऊंचाई एवं ज़मीन पर इसकी बिंदु से दूरी मिलकर एक त्रिभुज बनाते हैं।
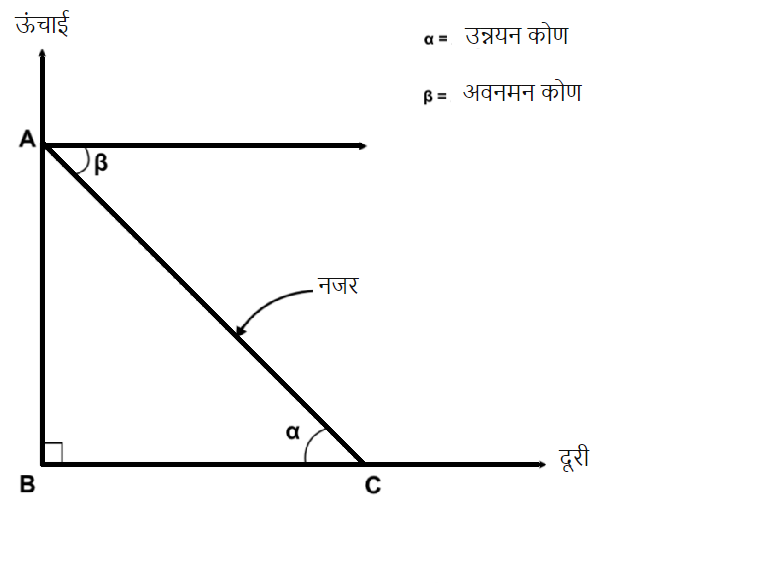
ऊपर चित्र में जैसा की आप देख सकते हैं यहाँ ऊंचाई AB रेखा से दर्शाई गयी है। देखने वाले एवं वास्तु के शीर्ष की दूरी AC से बताई गयी है। ऐसा ज़रूरी नहीं होता कि वह वस्तु हर बार ज़मीन से समलम्ब नहीं होती कभी तिर्यक भी हो सकती है। अब हम आगे देखते हैं कोण a दर्शक की नज़र का कोण है जो वास्तु के शीर्ष एवं दर्शक की आँख से बन रहा है। कोण b अवनमन कोण को दर्शा रहा है।
विभिन्न त्रिकोंमिति के माप (angle measurement in trigonometry)
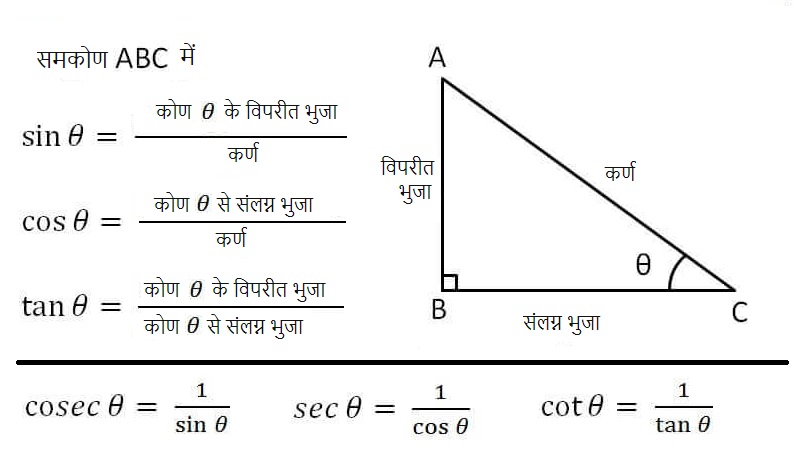
त्रिकोंमिति में कोणों का माप (angles in trigonometry)
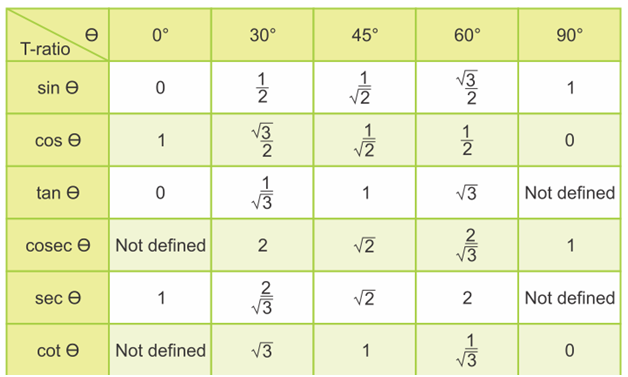
जैसा की आप ऊपर देख सकते की यहाँ ऊपर सारणी में हमें त्रिकोंमिति में कोण के विभिन्न माप दिए गए हैं जो की हमें सवाल हल करने के काम आयेंगे। अतः सवाल हल करते समय ये याद हैं तो हम आसानी से सवाल हल कर पायेगे।
ऊंचाई एवं दूरी प्रश्नावली (height and distance questions in hindi)
जैसा कि हम देखते हैं बहुत सी प्रतिस्पर्धा की परीक्षाओं में ऊंचाई एवं दूरी के सवाल आते हैं एवं अगर हमें त्रिकोंमिति आती है तो हम ऊंचाई एवं दूरी के सवालों को आसानी से हल कर सकते हैं। इसमें त्रिकोंमिति के ही सूत्र लगते हैं।
ऐसे सवालों में निचे दिए गए बिन्दुओं में से कोई दिए होते हैं आपको बस उन्हें पहचानना होता है वे हैं :
- वस्तु की दर्शक से दूरी
- वस्तु की ऊंचाई
- दर्शक का शीर्ष को देखने पर बन्ने वाला कोण (उन्नयन कोण)
- जब दर्शक ऊँचाई पर होता है एवं वास्तु का शीर्ष नीचे होता है तब जो कोण दर्शक की नज़र से बनता है (अवनमन कोण)
आपको बस सवाल में पहचानना है कि क्या कोनसा कोण है क्या ऊँचाई है आदि एवं आप बाकी सारी चीज़ें हल करके निकाल लेंगे।
उदाहरण:
उदाहरण 1: एक दर्शक की ऊँचाई 1.5 m है। वह एक टावर से 28.5 m दूर खड़ा है।दर्शक की आँख से टावर के शीर्ष का उन्नयन कोण 45 अंश का है। अब उस टावर की ऊंचाई ज्ञात कीजिये।
हल: आइये इस समस्या को हम एक चित्र बनाकर समझते हैं।
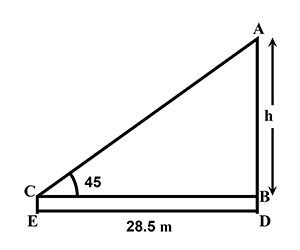
जैसा की आप ऊपर वाला चित्र देख कर पता लगा सकते है :
BD = CE = 1.5 m
त्रिभुज ABC में कोण CBA = 90 अंश
tan 45 = AB / BC
जैसा कि हम जानते हैं tan 45 का माप 1 होता है :
1 = AB / 28.5
AB = 28.5
अब,
h=AB+BD=28.5+1.5=30
अतः टावर की ऊंचाई 30 m है।
उदाहरण 2: एक व्यक्ति एक बिंदु P पर खड़ा होकर एक मीनार के शीर्ष को देख रहा है जिससे व्यक्ति की आँखों से शीर्ष पर अन्नयन कोण 30 अंश का बन रहा है। वह व्यक्ति मीनार कि तरफ कुछ दूर चलता है और अब उस मीनार के शीर्ष से उसकी आँखों पर 60 अंश का अन्नयन कोण बन रहा है। उस मीनार के तल की बिंदु P से ज्ञात कीजिये।
हल: आइये इसके आधार पर हम एक चित्र बनाते हैं।
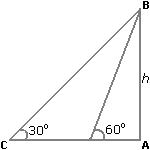
जैसा कि आपने देखा यह जानकारी सम्पूर्ण नहीं है तो इसमें या तो AB, AC या AD में से किसी एक का माप दिया रहना चाहिए था। अतः यह जानकारी सम्पूर्ण नहीं है। परीक्षा में ऐसे भी सवाल आ सकते हैं अतः आपको वह विकल्प चुनना है जिसमे लिखा रहे जानकारी पर्याप्त नहीं है।
इस लेख से सम्बंधित यदि आपका कोई भी सवाल या सुझाव है, तो आप उसे नीचे कमेंट में लिख सकते हैं।
गणित के अन्य लेख:
- बहुपद के शून्य और गुणनखंड कैसे निकालते हैं?
- भिन्नों को घटाना
- शेषफल प्रमेय
- बीजगणितीय सर्वसमिकाएँ क्या हैं?
- भिन्न का जोड़
- वर्ग का क्षेत्रफल
- मध्य बिंदु प्रमेय क्या होती है?
- घन की परिभाषा, गुणधर्म, क्षेत्रफल, आयतन