बीजगणितीय सर्वसमिकाएँ क्या हैं?

सर्वसमिकाएँ क्या होती हैं? (algebraic identities in hindi)

जैसा कि हम जानते हैं कि बीजगणित गणित की वह शाखा है जहां हम संख्याओं की जगह पर कुछ चिन्हों का प्रयोग करते है।

चिन्हों का प्रयोग करके हम बीजगणित में समीकरण बनाते हैं या उन समीकरणों को हल करते हैं। समीकरण बनाने से हम बड़ी गणनाओं को आसानी से कर पाते हैं।

सर्वसमिकाएँ किसी भी चर के ही विभिन्न मान होते हैं जिन्हें हम चर की जगह रखकर समीकरणों को बहुत आसानी से हल कर सकते हैं।

• जब हम समीकरणों में चार सर्वसमिकाएँ प्रयोग करते हैं तो ये समीकरणों को आसान बना देता है। इससे हम उस समीकरण को जल्दी हल कर पाते हैं।
• जल्दी हल होने से बड़ी गणना की मुश्किलें आसान हो जाती है। हम किसी बड़ी संख्या कि जगह पर चर रखते हैं तो वह गणना हमारे लिए आसान हो जाती है। जब हमें समीकरण भी मुश्किल लगता है तो हम उसे हल करने के लिए चर कि जगह उनका दूसरा कोई मन रखते हैं जिससे वह समीकरण और भी आसानी से हल हो जाता है।

उदाहरण (example of algebraic identities in hindi)

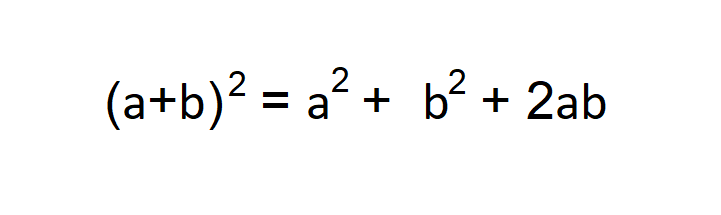
ऊपर दिए गए उदारहण में जैसा कि आप देख सकते हैं यहाँ a एवं b के वर्ग की एक सर्वसमिका दी गयी है।

जैसा कि हम देख सकते हैं यहाँ दो तरफ एक ही चर के दो मान हैं। हमे अगर किसी समीकरण में ऊपर वाला मान जोकि है:(a+b)² तो हम उसकी जगह ऊपर दिया गया मान लिख सकते हैं।

कुछ द्विपद बीजगणितीय सर्वसमिकाएँ (binomial theorem identities)

कुछ गुणनखंड बीजगणितीय सर्वसमिकाएँ (Three-variable Identities)

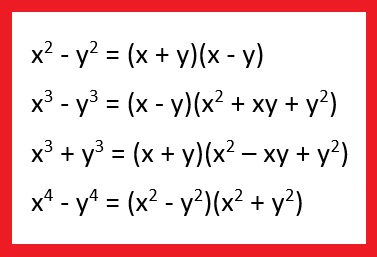
इस लेख से सम्बंधित यदि आपका कोई भी सवाल या सुझाव है, तो आप उसे नीचे कमेंट में लिख सकते हैं।